Высотные сети сгущения 4 страница

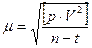
и сравнивают её с проектным значением ошибки единицы веса 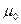; затем для любого параметра геодезического построения вычисляют вес и среднюю квадратическую ошибку уравненного значения этого параметра

.

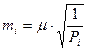В нивелирных сетях значения всех частных производных измерений равны либо плюс единице, либо минус единице, либо нулю, так как превышение по линии равно разности отметок реперов в конце линии и в её начале

;

если один из реперов – начальный или конечный, - является исходным, то частная производная по его отметке равна нулю. Уравнения поправок содержат в левой части всего два члена (или один член) с неизвестными поправками в отметки реперов. Приближённые значения отметок вычисляют обычно по измеренным превышениям, начиная от исходных реперов, поэтому часть свободных членов параметрических уравнений поправок будут равны нулю.

В матричной записи параметрический способ МНК-уравнивания имеет вид

- параметрические уравнения поправок ;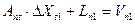

- нормальные уравнения параметров-поправок ;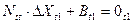

- матрица коэффициентов нормальных уравнений ;

- вектор свободных членов нормальных уравнений ;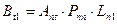

- вектор поправок к приближённым значениям неизвестных .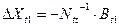

В этих формулах:

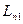- вектор свободных членов параметрических уравнений поправок, ;

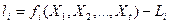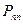- диагональная матрица весов измерений;

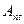- матрица коэффициентов параметрических уравнений поправок размером 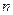строк и 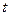столбцов.

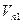- вектор поправок в результаты измерений.

2.7. Проектирование нивелирования III класса

Перед составлением проекта на нивелирование любого класса собирают и анализируют все материалы ранее выполненных нивелировок на территории проектируемых работ. Сведения об этих работах можно получить в территориальных инспекциях Госгеонадзора.

Проект составляется в соответствии с требованиями Инструкции по нивелированию и, если нивелирование III класса проектируется для обеспечения топографических съёмок масштаба 1:5000 и крупнее, то нужно учитывать ещё и требования Инструкции по топографическим съёмкам.

Проектирование выполняют на топографических картах масштаба 1:100 000 – 1:200 000; в случае необходимости проект уточняют в деталях на картах более крупных масштабов. На карту нужно нанести все выполненные ранее работы по нивелированию, а также все пункты триангуляции и полигонометрии; наносят также проектируемые пункты триангуляции и полигонометрии. В любом случае проектирование нивелирования III класса производится в пределах полигонов нивелирования II класса.

Желательно совмещать проектируемые линии нивелирования с ходами полигонометрии, прокладываемыми с целью развития и сгущения геодезических сетей.

Наиболее подробно разрабатывают проекты связи новых линий нивелирования с существующими линиями. Начало и конец проектируемой линии должны быть просто и надёжно связаны с существующими линиями более высокого или того же класса. Проектируемая линия должна быть надёжно связана с пересекаемыми ею линиями нивелирования всех классов. Связь проектируемых линий III и IY классов с существующими линиями I, II, III, IY классов осуществляется путём включения в ход одного репера существующей линии.

На каждый образуемый узел связи линий нивелирования составляют особую схему в достаточно крупном масштабе, на которой показывают направления всех связываемых линий и существующие реперы, подлежащие включению в проектируемую линию.

В соответствии с конкретными климатическими и почвенными условиями района работ из сборника “Типы центров” выбирают конструкции реперов проектируемых линий.

Нивелирование через водные препятствия проектируют в наиболее узких местах с использованием мелей и островов. Если ширина водного препятствия превышает 150 метров, то на обоих берегах предусматривают закладку реперов – по одному на каждом берегу. Каждый репер по возможности намечают в незатопляемой зоне; превышение между этими реперами не должно быть больше 0,5 м.

При проектировании высотной основы морских уровенных и основных речных постов следует помнить, что уровенный пост должен быть оборудован не менее, чем тремя реперами: двумя основными (один из них фундаментальный) и одним рабочим. Основные реперы служат для проверки положения рабочего репера и для закрепления нуля поста. В качестве основных реперов используют реперы, находящиеся не далее 3 км от поста. Рабочий репер, предназначенный для систематического контрольного нивелирования измерительных устройств, располагают в непосредственной близости от этих устройств и вне зоны затопления высокими водами.

Нивелирование через водные препятствия шириной до 200 м выполняют по обычной методике двумя приёмами с соблюдением равенства расстояний до задней и передней реек. Между приёмами изменяют высоту нивелира на (3 – 5) см. Расхождение превышений между приёмами допускается 4 мм для III класса и 7 мм для IY класса.

При ширине препятствия (200 – 400) м нивелирование выполняют нивелиром с плоскопараллельной пластинкой способом совмещений; при этом применяют особые щитки на рейку. Щиток должен иметь два штриха, расположение которых определяется из специальных исследований, и жёстко крепиться на рейке.

Передачу высоты выполняют две бригады с двух берегов по двум створам с использованием двух нивелиров и двух комплектов инварных реек. При этих измерениях должен присутствовать начальник партии и главный инженер или начальник экспедиции. Расхождение между превышениями, измеренными разными наблюдателями по разным створам, не должно превышать 5 мм для III класса нивелирования.

Измерение превышений через препятствие шириной более 400 м выполняют способом подвижной марки, однако, лучше всего делать такую передачу высоты приборами и по методике II класса нивелирования.

Иногда в исключительных случаях нивелирование III и IY классов через препятствия выполняют по льду, соблюдая следующие правила:

- ход выбирают по наиболее короткому пути и выполняют измерения в кратчайшие сроки (за один день);

- на обоих берегах заблаговременно закладывают по одному постоянному реперу;

- перед началом работы очищают трассу от снега и в местах установки реек пробивают во льду отверстия и вмораживают в них деревянные колья длиной (20 – 30) см с вбитыми в их торцы гвоздями со сферической шляпкой;

- нивелирование по льду выполняют два раза в прямом ходе и два раза в обратном ходе;

- нивелировать нужно в периоды наименьших суточных колебаний уровня льда и использовать результаты наблюдений метеопостов и водопостов;

- во время нивелирования нужно наблюдать за движением льда по отдельной рейке, вмороженной в лёд на расстоянии 50 м от берега, и в результаты измерения превышений вводить поправки за движение льда.

2.9. Поиск грубых ошибок измерений в нивелирных сетях

Понятие “грубая ошибка измерения” вводится на начальном этапе изучения теории ошибок и теории математической обработки геодезических (и иных) измерений. Под грубой ошибкой понимают случайную ошибку измерения, которая по своему абсолютному значению превышает установленный для случайных ошибок допуск 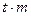, где 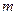-средняя квадратическая ошибка одного измерения, 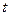- коэффициент доверительной вероятности, принимаемый равным либо 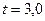(с вероятностью 99,7%), либо (с вероятностью 98,8%), либо 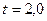(с вероятностью 95,4%). Процент вероятности означает, что именно с такой вероятностью измеренное или вычисленное значение 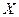какой-либо величины находится в интервале от 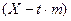до 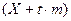. Поиск грубых ошибок измерений на практике осложняется тем, что истинные значения случайных ошибок неизвестны, и, если среди случайных ошибок есть грубые ошибки, то об этом можно узнать только по косвенным признакам. К таким признакам можно отнести:

- недопустимо большое значение одной или более невязок условных уравнений связи при коррелатном способе уравнивания;

- недопустимо большое значение свободных членов при рекуррентном способе уравнивания;

- несоизмеримо большие по сравнению с точностью измерений поправки, полученные при уравнивании геодезического построения;

- увеличение средней квадратической ошибки единицы после уравнивания по сравнению с её проектным значением.

В реальном геодезическом построении грубая ошибка может либо маскироваться (ослабляться) на фоне остальных случайных ошибок, либо, наоборот, демаскироваться (усиливаться).

В широком смысле проблема борьбы с грубыми ошибками распадается на несколько отдельных задач:

- установить, есть ли в данном геодезическом построении грубые ошибки вообще (одна или более), или их нет. Если грубые ошибки сесть, то следует решать следующие задачи;

- определить конкретные измерения, в которых имеются грубые ошибки – то есть, локализовать положение грубых ошибок с точностью до одного измерения; если это невозможно, то следует попытаться локализовать положение грубых ошибок с точностью до небольшой группы измерений;

- оценить значения грубых ошибок измерений;

- принять меры к ослаблению или полному устранению влияния грубых ошибок измерений на результаты уравнивания данного геодезического построения.

К настоящему времени разработано достаточно много методик по обнаружению и учёту грубых ошибок измерений; некоторые из них базируются на стандартной теории обработки измерений, другие - используют сложные разделы математики с привлечением произвольно назначаемых параметров. Вторую группу составляют так называемые “робастные методы обработки измерений”. В большинстве робастных методик уравнивание выполняется циклами; результаты очередного цикла анализируются, и поправки в измерения сортируются по их величине; затем для части измерений веса пересчитываются, и уравнивание выполняется вновь. Циклы повторяются до тех пор, пока все поправки в измерения будут удовлетворять условию, содержащему тот самый произвольно назначенный параметр.

Все робастные методы являются реализацией принципа обратной связи, схема которого изображена на рис.23. Традиционный путь получения и обработки геодезической информации – это 1 – 2 – 3 – 4 – 1 (через повторные измерения, если в сети обнаружены грубые ошибки измерений). Принцип обратной связи предполагает другой маршрут 1 – 2 – 3 – 4 – 5 – 2. По Инструкции изменять результаты измерений без их повторения запрещено; поэтому остаётся один выход – изменять веса измерений. По существу веса или ошибки измерений назначаются априорно на основе опыта подобных измерений в прошлом. Поэтому корректировка весов измерений является логически обоснованным решением задачи уравнивания геодезических измерений, содержащих с грубые ошибки.

Применение робастных методов в геодезии многие ведущие учёные не рекомендуют.

Рисунок 23 - Схема принципа обратной связи обработки информации

Для поиска грубых ошибок в нивелирных сетях наиболее просто и доступно вычислить высотные невязки всех полигонов, выписать их на схему сети и выполнить визуальный анализ невязок. Наличие в двух соседних полигонах больших невязок с противоположными знаками свидетельствует о грубой ошибке измеренного превышения по линии, являющейся общей для обоих полигонов. В отдельных случаях можно обнаружить грубые ошибки в двух превышениях одного полигона, но сложные комбинации грубых ошибок визуально локализовать практически невозможно. Наиболее действенным контролем грубых ошибок измерений в любом геодезическом построении, в том числе и в нивелирной сети, является тестирование сети по методу наложения графиков поправок (МНГП). Теория этого метода разработана на кафедре геодезии СГГА под руководством Б.Н. Дьякова в 2002 году. Изложим кратко эту теорию.

В параметрическом уравнивании по МНК матрица обратных весов поправок выражается формулами

Q_V=P^-1–A·R^-1·A^T,

или

Q_V=G·P^-1, (2.4)

где P^-1- матрица обратных весов измерений размером n´ n (n – количество измерений); A - матрица коэффициентов параметрических уравнений поправок размером n ´ k (k – количество неизвестных);

R^-1 – матрица, обратная матрице коэффициентов нормальных уравнений, размером k ´ k; G -матрица выполняет роль матрицы-преобразователя вектора P^-1 в матрицу Q_V.

Дата добавления: 2014-12-07