После умножения выражения (2.4) слева на матрицу P получим

G = Q_V· P,

или

G=E–A·R^-1·A^T·P

где E – единичная матрица размером n´ n (n – количество измерений);

P – диагональная матрица весов измерений размером n´ n.

Матрица G – квадратная, размером n´ n, вырожденная, идемпотентная; в теории параметрического уравнивания она применяется в нескольких матричных уравнениях. Для наших исследований мы использовали уравнение

V=–G ∙ Δ, (2.5)

в котором: V – вектор поправок в измерения, получаемый из уравнивания;

D - вектор истинных ошибок измерения, а G -матрица выполняет роль матрицы-преобразователя вектора D в вектор V.

Уравнение (2.5) означает, что поправку V_i каждого измерения можно представить в виде линейной комбинации истинных ошибок измерений

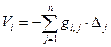, (2.6)

где g_i,j – элементы i -той строки G -матрицы.

При отсутствии в геодезической сети грубых ошибок измерений истинные ошибки D_j, произведения g_i,jD_j и поправки V_i являются случайными величинами, и их математические ожидания равны нулю.

Если среди измерений есть хотя бы одно грубое с истинной ошибкой D_j, то одно слагаемое в формуле (2.6) будет иметь ненулевое математическое ожидание, так как 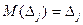и

,

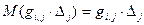а формулу (2.6) можно переписать в виде

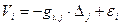, (2.7)

где e_i – суммарное влияние случайных ошибок остальных измерений; понятно, что

.

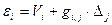Построим график поправок V_i (по горизонтальной оси откладываются номера измерений i) и график величин (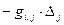) и наложим второй график на первый. Их несовпадение в каждой точке графика равно величине e_i, следовательно, можно вычислить среднее квадратическое отклонение несовпадения этих графиков

.

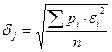Истинная ошибка D_j вычисляется с некоторой погрешностью из формулы (2.7) при i=j и M(e_j)=0

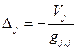. (2.8)

Ввиду того, что величина e_i является случайной составляющей поправок V_i, для d_j существует предел d₀ , вычисляемый по формуле

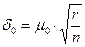, (2.9)

где m₀ - проектное значение ошибки единицы веса; r – количество избыточных измерений (r=n-k).

Дата добавления: 2014-12-07