Анализ возможностей сети Петри для моделирования процессов развития современного авиапредприятия

Реальные системы состоят из разнообразных компонентов, различающихся физическими свойствами, функциональным назначением, сложностью внутренней структуры. Для того чтобы сконструировать адекватный математический аппарат, предназначенный для моделирования систем, необходимо [21]::

· установить круг качественных и количественных задач, которые должны решаться с помощью моделей, например — выполняет ли система те функции, для которых она предназначена; функционирует ли она эффективна; можно ли упростить систему, не нарушая ее общего функционирования; можно ли из заданных систем сконструировать более сложную, отвечающую заданным требованиям и т.д.;

· осуществить переход от физических и функциональных особенностей компонентов системы к их абстракциям, сначала в форме некоторого набора концептуальных понятий, затем— в точных математических терминах.

Компоненты структуры авиапредприятия и их действия представляются абстрактными событиями такими, например, как завершение этапа проекта, продажа старого оборудования, поиск потенциальных исполнителей модернизации.

Событие может произойти один раз (применительно в авиапредприятия можно выделить, например, проведение тендеров на закупку оборудования), повториться многократно (подготовка (обучение) сотрудников), порождая конкретные действия, или не произойти ни разу. Совокупность действий, возникающих как реализации событий при функционировании системы, образуют процесс, порождаемый этой системой. В общем случае одна и та же система может функционировать в одних и тех же условиях по-разному, порождая некоторое множество процессов, т.е. функционировать недетерминировано.

Реальная система функционирует во времени, события происходят в некоторые моменты времени и длятся некоторое время. В синхронных моделях систем события явно привязаны к определенным моментам или интервалам времени, в которые происходит одновременное изменение состояний всех компонентов системы, трактуемое как изменение общего состояния системы. Смена состояний в указанных моделях происходит последовательно. Этот подход к моделированию сложных организационно-технических систем имеет ряд недостатков:

· в большой системе приходится учитывать состояние всех компонентов при каждой смене ее общего состояния, что делает модель громоздкой;

· при таком подходе исчезает информация о причинно-следственных связях между событиями в системе; такие понятия, как конфликты между компонентами системы (из-за ресурсов) или ожидание одним из компонентов результатов работы других компонентов, трудно выражаются в терминах смены состояний системы;

· в так называемых асинхронных системах события могут происходить внутри неопределенно больших интервалов времени, заранее трудно или нельзя указать более точно время их начала, конца и длительность.

Выходом может служить отказ от введения в модели систем времени и тактированных последовательностей изменений состояний, а замена их — причинно-следственными связями между событиями. Модели такого типа, в том числе сети Петри (теория сетей Петри разработана немецким математиком Карлом-Адамом Петри в диссертационной работе «Взаимодействующие автоматы» в 1962г), называют асинхронными. В указанных моделях если возникает необходимость осуществить привязку ко времени, то моменты или интервалы времени представляют как события. Замена временных связей причинно-следственными связями дает возможность более наглядно описать структурные особенности функционирования систем.

Отказ от времени приводит к тому, что события в асинхронной модели рассматриваются или как элементарные (неделимые, мгновенные), или как составные, имеющие некоторую внутреннюю структуру, образованную из подсобытий.

Взаимодействие событий в больших асинхронных системах (в нашем случае бизнес-система авиапредприятия) имеет, как правило, сложную динамическую структуру. Эти взаимодействия описываются более просто, если указывать не непосредственные связи между событиями, а те ситуации, при которых данное событие может реализоваться. При этом глобальные ситуации в системе формируются с помощью локальных операций, называемых условиями реализации событий.

Условие имеет емкость:

· 0— не выполнено;

· 1— выполнено;

· n— условие выполнено с n-кратным запасом.

Условие соответствует таким ситуациям в моделируемой системе, как оформление документов на модернизацию. Определенные сочетания условий разрешают реализоваться некоторому событию (предусловия события), а реализация события изменяет некоторые условия (постусловия события), т.е. события взаимодействуют с условиями, а условия — с событиями.

Таким образом, предполагается, что для решения задач достаточно представить системы как структуры, образованные из элементов двух типов — событий и условий.

В сетях Петри события и условия представлены абстрактными символами из двух непересекающихся алфавитов, называемых соответственно множеством переходов и множеством позиций. Условия-позиции и события-переходы связаны отношением непосредственной зависимости (непосредственной причинно-следственной связи), которое изображается с помощью направленных дуг, ведущих из позиций в переходы и из переходов в позиции. Позиции, из которых ведут дуги на данный переход, называются его входными позициями, а позиции, на которые ведут дуги из данного перехода, — выходными позициями.

Выполнение условия изображается разметкой соответствующей позиции, а именно помещением числа n или n маркеров (фишек) в это место, где n>0 — емкость условия.

Динамика поведения моделируемой системы находит свое отражение в функционировании сети Петри. Неформально работу сети можно представить как совокупность локальных действий (в нашем случае таких как подготовка помещений, покупка нового оборудования, продажа старого оборудования внедрение и опытная эксплуатация), которые называются срабатываниями переходов. Они соответствуют реализациям событий и приводят к изменению разметки позиций, т.е. к локальному изменению условий в системе.

Переход может сработать, если выполнены все условия реализации соответствующего события. Срабатывание перехода — это неделимое действие, изменяющее разметку его входных и выходных позиций. В процессе функционирования сети происходит смена разметок мест как результат срабатывания ее переходов. Сеть останавливается, если ни один из ее переходов не может сработать.

Таким образом, сети Петри формализуют понятие абстрактной асинхронной системы— динамической структуры из событий и условий.

Сетью Петри называется ориентированный двудольный (бихроматический) граф G_p=(P, T, K, S), в котором P и T — два множества вершин, причем P={p_i} — множество вершин позиций p_i, T={t_j} — множество вершин переходов t_j (P Ç T = Æ), соединенных между собой дугами K = P ´ T È T ´ P по функциональным правилам S [22].

В общем случае функциональные правила S включают матрицы инциденций и ингибиторных дуг, вектора (функции) начальной маркировки, временных задержек и приоритетов переходов.

В зависимости от функциональных правил S формируется требуемая интерпретация сетей Петри, обусловливающая ее конкретное применение.

Можно указать три эквивалентных способа задания сетей Петри:

· графический;

· аналитический (теоретико-множественный);

· матричный.

Графический способ.Множество элементов P графа Петри G_p, часто обозначаемого PN, изображаются кружками, а множество T — утолщенными короткими прямыми линиями. Множество дуг, которое соответствует множествам упорядоченных пар вершин (p_i, t_j) и (t_j, p_i) называют множеством дуг K графа PN.

Графическое изображение вершин переходов также может быть представлено в виде квадратов или прямоугольников.

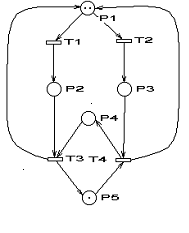
Рис 4. Графический способ задания сетей Петри.

Логические условия процесса задаются правилами движения маркеров через переходы:

1. Если к переходу T_j подходит более одной дуги, то он открывается после выполнения последней операции в позициях, из которых к нему подходят дуги.

2. Дуга может иметь кратность, соответствующую числу проходящих через нее маркеров. Переход разрешен, если число маркеров во входной позиции не меньше

3. Если к переходу подходит несколько дуг, а выходит одна дуга, то несколько маркеров сливаются в один. Если к переходу подходит одна дуга, а выходят несколько дуг, то после перехода один маркер делится на несколько по числу дуг.

4. Переходы могут иметь разные приоритеты (pr). В этом случае маркер сначала движется через переход с более высоким приоритетом.

5. Ингибиторная дуга (с кружком вместо стрелки) запрещает открывание перехода T_j, если в позиции, откуда она выходит, имеется маркер.

Маркеры и переходы могут иметь разную окраску. При этом маркеры определенного цвета могут двигаться через переходы такого же цвета.

Аналитический способ. Говорят, что задана сеть Петри:

P_N = (P, T, K, S), (1)

если заданы множества P, T, K и отображение

S: ((P ´ T) È (T ´ P)) ® K (2)

Часто отображение S несет не только указанную функцию, но и включает правила соединения вершин между собой и правила, отражающие обход ветвей сети при практической реализации P_N. Если число вершин p_i и t_j конечно, то сеть Петри называется конечной, в противном случае — бесконечной.

Пусть заданны конечные множества P = {p₁, p₂,..., p_n}и T = {t₁, t₂,..., t_k}. Из определения сетей Петри и функциональных правил S следует, что Q = P ´ T и R = T ´ P, тогда выражение (2) можно представить в виде: S: (Q È R) ® K.

Здесь множества Q и R для каждых пар вершин (p_i, t_j) и (t_j, p_i) включают соответственно подмножества дуг K^Op_i Î Q или K^It_j Î Q и K^Ip_j Î R или K^Ot_j Î R (O — output, I — input). Подмножество дуг (p_i, t_j), выходящих из вершины p_i, обозначается K^Op_i, а входящих в t_j — K^It_j. Подмножество дуг (t_j, p_i), выходящих из вершины t_j, обозначается K^Ot_j, а входящих в p_i — K^Ip_j.

Часто возникает необходимость указания всех вершин t(p), входящих в вершину p_i(t_j) или выходящих из вершины p_i(t_j). Подмножество T^Op_i включает все вершины t_n, к которым направлены дуги из K^Op_i от вершины p_i, а подмножество T^Ip_i содержит все вершины t_m (t_m, t_n Î T), от которых дуги из K^Ip_j направлены к вершине p_i. Аналогично подмножества P^It_j содержат все вершины p_k, дуги от которых из K^It_j направлены к t_j, а подмножество P^Ot_j — все вершины p_l, дуги к которым из K^Ot_j направлены от t_j (p_k, p_l Î P).

Матричный способ. Структура сети задается матрицей инциденций, элементами которой являются числа

Aij =

| К, если дуга К-й кратности выходит из | перехода Tj и выходит в позицию Pi; | К, если дуга К-й кратности выходит из | позиции Pi и входит в позицию Tj; | 0, если Tj и Pi не соединены дугой.

Параметры состояния технологического процесса задаются вектором исходного распределения маркеров по n позициям сети

М_о = (P₁, P₂, P₃,..., P_n),

где

Pi =	| 0, когда в Pi нет маркера; | | 1, когда в Pi есть маркер;

вектором задержек Z_i маркеров в позициях (временем выполнения операций):

M_z = (Z₁, Z₂, Z₃,..., Z_n),

вектором приоритетов переходов

M_pr = (pr₁,pr₂,pr₃,...,pr_n),

где pr_i — приоритет соответствующего перехода;

и матрицей ингибиторных дуг ING_i,j из элементов:

INGi,j =

| 1, если дуга между позицией Pi и | переходом Tj - ингибиторная; | | 0, если дуга между позицией Pi и | переходом Tj - неингибиторная;

Таким образом, если сеть Петри задана одним из описанных выше способов (графическим, аналитическим или матричным), можно перейти к любому другому способу задания, а результаты, полученные с помощью одного, можно интерпретировать для другого. Наиболее часто сети Петри задаются графическим способом, отражая наглядность, полноту и однозначность решаемой задачи. При исследованиях сетей Петри с помощью ЭВМ используют аналитический или матричный способ задания.

При проведении исследований в рамках данной дипломной работы мы использовали графический способ задания сети Петри, описывающей альтернативные сценарии модернизации авиапредприятия. Данный способ задания сети Петри, базировался на инструментальных средствах, предоставляемых программным комплексом Multi-objective optimization, разработанным в Военно-Космической Академии им. А.Ф. Можайского

Дата добавления: 2014-11-29