Угол между прямыми. Условия параллельности и

Неполные уравнения прямой.

Уравнение (7.4) называется полным, если коэффициенты А,В и С не равны нулю, и неполным, если хотя бы одно из этих чисел равно нулю. Рассмотрим возможные виды неполных уравнений прямой.

1) С = 0 - прямая Ах + Ву = 0 проходит через начало координат.

2) В = 0 - прямая Ах + С = 0 параллельна оси Оу (так как нормаль к прямой { A,0} перпендикулярна оси Оу).

3) А = 0 - прямая Ву + С = 0 параллельна оси Ох.

4) В=С =0 – уравнение Ах = 0 определяет ось Оу.

5) А=С =0 – уравнение Ву = 0 определяет ось Ох.

Таким образом, прямая, задаваемая полным уравнением, не проходит через начало координат и не параллельна координатным осям. Преобразуем полное уравнение прямой следующим образом:

Ах + Ву + С = 0 |:(- C), 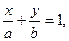(7.9)

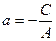где и 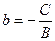равны величинам отрезков, отсекаемых прямой на осях Ох и Оу. Поэтому уравнение (7.9) называют уравнением прямой в отрезках.

перпендикулярности двух прямых.

1. Если прямые L₁ и L₂ заданы общими уравнениями

А₁х + В₁у + С₁ = 0 и А₂х + В₂у + С₂ = 0,

то угол между ними равен углу между их нормалями, то есть между векторами {A₁,B₁} и {A₂,B₂}. Следовательно,

. (7.10)

Условия параллельности и перпендикулярности прямых тоже сводятся к условиям параллельности и перпендикулярности нормалей:

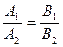- условие параллельности, (7.11)

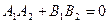- условие перпендикулярности. (7.12).

2. Если прямые заданы каноническими уравнениями (7.5), по аналогии с пунктом 1 получим:

, (7.13)

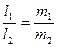- условие параллельности, (7.14)

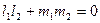- условие перпендикулярности. (7.16).

Здесь 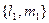и 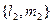- направляющие векторы прямых.

3. Пусть прямые L₁ и L₂ заданы уравнениями с угловыми коэффициентами (7.8)

у = k₁x +b₁ и y = k₂x + b₂, где 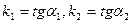, а α₁ и α₂ – углы наклона прямых к оси Ох, то для угла φ между прямыми справедливо равенство: φ = α₂ - α₁. Тогда

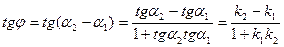. (7.17)

Условие параллельности имеет вид: k₁=k₂, (7.18)

условие перпендикулярности – k₂=-1/k₁, (7.19)

поскольку при этом tgφ не существует.

Расстояние от точки до прямой.

Рассмотрим прямую L и проведем перпендикуляр ОР к ней из начала координат (предполагаем, что прямая не проходит через начало координат). Пусть n – единичный вектор, направление которого совпадает с ОР. Составим уравнение прямой L, в которое входят два параметра: р – длина отрезка ОР и α – угол между ОР и Ох.

у Для точки М, лежащей на L, проекция вектора ОМ на прямую

L ОР равна р. С другой стороны, пр_nOM=n·OM. Поскольку

Р n ={cos α, sin α }, a OM ={ x,y }, получаем, что

n M x cosα + y sinα = p, или

О х x cosα + y sinα ­­- p = 0 - (7.20)

- искомое уравнение прямой L, называемое нормальным

уравнением прямой (термин «нормальное уравнение» связан

с тем, что отрезок ОР является перпендикуляром, или нормалью, к данной прямой).

Определение 7.2. Если d – расстояние от точки А до прямой L, то отклонение δ точки А от прямой L есть число + d, если точка А и начало координат лежат по разные стороны от прямой L, и число – d, если они лежат по одну сторону от L.

Теорема 7.1. Отклонение точки А(х₀,у₀) от прямой L, заданной уравнением (7.20), определяется по формуле:

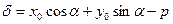. (7.21)

Доказательство.

у Q Проекция OQ вектора ОА на направление ОР равна

P A n·OA =x₀ cosα + y₀ sinα. Отсюда δ = PQ=OQ-OP=OQ-p =

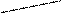
n x₀ cosα + y₀ sinα - p, что и требовалось доказать.

O

L

Следствие.

Расстояние от точки до прямой определяется так:

(7.22).

Замечание. Для того, чтобы привести общее уравнение прямой к нормальному виду, нужно умножить его на число , причем знак выбирается противоположным знаку свободного члена С в общем уравнении прямой. Это число называется нормирующим множителем.

Пример. Найдем расстояние от точки А (7,-3) до прямой, заданной уравнением

3 х + 4 у + 15 = 0. А ² + B ²=9+16=25, C =15>0, поэтому нормирующий множитель равен

-1/5, и нормальное уравнение прямой имеет вид: Подставив в его левую часть вместо х и у координаты точки А, получим, что ее отклонение от прямой равно

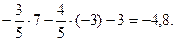Следовательно, расстояние от точки А до данной прямой равно 4,8.

Дата добавления: 2014-12-07