Законы распределений случайных величин

Большинство СВ подчиняется тому или иному закону распределения, знание которого позволяет предвидеть вероятности попадания исследуемой СВ в определенные интервалы. Это необходимо чтобы осуществлять продуманную экономическую политику с учетом возможности возникновения той или иной ситуации. Очень часто реальные данные самой различной природы описываются нормальным законом распределения. Эта закономерность проявляется всегда, когда конечный результат определяется достаточно большим числом факторов, среди которых нет доминирующего. Тогда чем больше отклонение от средней величины, тем реже встречаемость таких отклонений при любых законах распределения отдельных факторов.

Предположим, монета подбрасывается 100 раз. И каждый раз она можете равным успехом выпасть «орлом» пли «решкой». Какова вероятность того, что в результате этой игры выпадет 0 «орлов», или 1 «орел»,..., 10 «орлов»? Де Муавру еще в XVIII веке удалось доказать, что при большом числе наблюдений уравнение кривой для любой подобной задачи описывается следующей формулой:

Отметим, что только два параметра: среднее значение и стандартное отклонение отличают друг от друга бесконечное множество нормальных кривых, одинаковой формы.

Среднее значение задает положение кривой на числовой оси, а стандартное отклонение определяет ширину этой кривой.

Получим единичное нормальное распределение, которое используется как стандарт — эталон. Его среднее значение 0 а стандартное отклонение 1. Его часто называют стандартным нормальным распределением. Кривая симметрична относительно Хср=0.

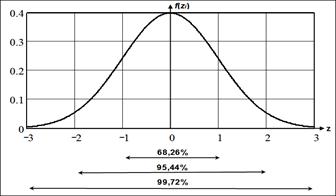
Площадь под кривой рaвнa 1, поэтому вероятность попадания СВ в заданный диапазон равна площади под кривой, лежащей между соответствующими точками, определяющими границы этого диапазона. Например, вероятность того, что отклонение от среднего значения не превысит удвоенного среднеквадратического отклонения составляет 95,44%,

Наиболее часто встречаются значения признака, близкие к его среднему. По мере удаления от среднего значения число наблюдений или вероятность наступления события уменьшаются. Причем в интервал от ` х-s<sub>х</sub> до ` х+s_х попадает 68,3% случаев; от ` х- 2 s<sub>х</sub> до ` х+ 2 s_х – 95,5%; от ` х- 3 s<sub>х</sub> до ` х+ 3 s_х – 99,7% случаев. Поскольку в последний интервал попадает подавляющее большинство случаев при нормальном распределении, и называется иногда правилом «трех сигм».

Пример:

№
Надой, ц
Надой, ц

min=18 max=41 хср=36 σ_x=6,3

Хср-3σ_x=17,2 Хср+3σ_x=54,8

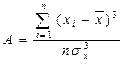Чтобы оценить степень отклонения графика распределения частот от симметричного вида относительно среднего значения используется такой показатель как асимметрия, который вычисляется по формуле:

Для симметричного распределения асимметрия равна 0. Если чаще встречаются значения меньше среднего, то говорят о левосторонней, или положительной асимметрии (As> 0). Если же чаше встречаются значения больше среднего, то асимметрия – правосторонняя, или отрицательная (As<0). Чем больше отклонение от нуля, тем больше асимметрия.

Для характеристики степени плосковершинности или остроконечности графика распределения служит показатель эксцесса, который определяется формулой:

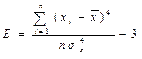Вид распределения частот при разных значениях асимметрии и эксцесса показан на рисунке.

Для нормального распределения и асимметрия и эксцесс равны нулю.

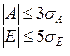Распределение принимают за нормальное, если выполняются следующие неравенства:

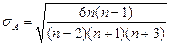Где

стандартная ошибка ассиметрии

стандартная ошибка эксцесса

Упрощенно можно принять:

При моделировании экономических процессов используются СВ, которые представляют собой алгебраическую комбинацию нескольких СВ. Для прогноза поведения таких СВ часто используется χ² - распределение и распределение Cтьюдента.

χ² - распределение получается при суммировании квадратов n СВ, имеющих стандартное нормальное распределение. Между этими СВ могут быть m линейных зависимостей.

Распределение Cтьюдента (t -распределение) с числом степеней свободы n определяется как:

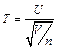
Где U имеет стандартное нормальное распределение, а V– независимая СВ распределенная по закону χ2 с n степенями свободы. Этот параметр полностью определяет характер распределения. При n > 30 распределение Cтьюдента практически совпадает с нормальным.

Дата добавления: 2014-12-07