Лекция № 6 теории относительности Эйнштейна

23. Предпосылки возникновения специальной теории относительности Эйнштейна

Оказалось, что уравнения Дж. Максвелла, описывающие элек­тромагнитное поле, неинвариантны при переходе из одной инерци-альной системы в другую относительно преобразований Галилея. Следует сказать, что именно эта неинвариантность и вызвала новый всплеск концепций с принятием эфира, и в конечном счете - опыт Майкельсона. Различный спектр мнений и предложений, возник­ших с связи с вышеуказанной коллизией «неподчинения уравнений Максвелла механическому принципу относительности», можно выразить тремя основными точками зрения:

1. Согласно первой следует отказаться от уравнений Максвел­ла или внести в них необходимые поправки, лишь бы сде­лать их инвариантными относительно Галилеевых преоб­разований. Однако уравнения Максвелла демонстрировали высочайшую степень совпадения теории с экспериментом, а все вносимые поправки оказывались неподтверждаемыми.

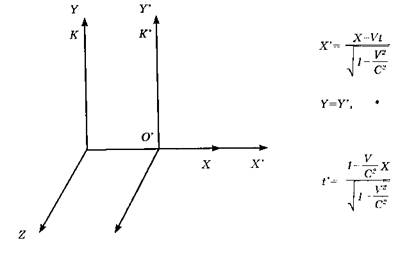
2. Вторая точка зрения отстаивалась А. Пуанкаре и Г. Герцем, считавшими принцип относительности обязательным для описания не только механических явлений, но и электро­магнитных. В 1890 г. Герц принимает гипотезу, высказанную ранее Д. Стоксом, о существовании эфира, полностью увлекающегося движущимися телами. Исходя из этих принципов, он находит уравнения, инвариантные по отно­шению к галилеевым преобразованиям координат и време­ни при переходе из одной инерциальной системы отсчета в другую. В частном случае покоящегося тела эти уравнения переходят в уравнения Максвелла. Герц получил наиболее очевидное обобщение теории Масвелла на случай движу­щихся тел, но оно оказалось несовместимым с результатом эксперимента, ибо противоречило эксперименту Физо по распространению света в движущейся жидкости. 3. Точка зрения, отстаиваемая X. Лоренцем. Известно, что Ло­ренц являлся сторонником атомной теории строения веще­ства, а после открытия в 1897 г. У. Томсоном отрицательно заряженной частицы - электрона - создал теорию, в кото­рой уравнения Максвелла включают в себя идею о дискрет­ной структуре электричества. При этом Лоренц использует гипотезу эфира, рассматривая электромагнитное поле как свойство эфира, противопоставляя его состоящему из элект­рически заряженных частиц веществу. Лоренцу удалось всю электродинамику покоящихся и движущихся тел свести к уравнениям Максвелла, дать на этой основе объяснение большому числу экспериментальных фактов. Но при этом он вводит абсолютно покоящуюся выделенную среди прочих систему отсчета, связанную с неподвижным эфиром, в ко­торой только и выполняются уравнения Максвелла. Таким образом, точка зрения, отстаиваемая Лоренцем, говорила о несостоятельности самого принципа относительности. На место абсолютного пустого неподвижного ньютоновского пространства он ставит абсолютное тело отсчета - непод­вижный эфир, то есть вводит привилегированную систему отсчета. Однако все имеющиеся опытные данные свидетель­ствовали в пользу принципа относительности, в том числе и опыт А. Майкельсона, свидетельствовали об эквивалентно­сти всех инерциальных систем отсчета, кроме этого, назван­ный опыт устанавливал факт постоянства скорости света в любой системе отсчета. А. Эйнштейн писал, что «специаль­ная теория относительности обязана своим происхождением этой трудности, которая ввиду ее фундаментального харак­тера казалась нетерпимой. Следует сказать, что X. Лоренц (и ряд других физиков, среди которых Д. Лармор, Фицдже-ральд и др.) предпринимали многочисленные попытки, пы­таясь согласовать отрицательный результат опыта Майкель­сона с идеей абсолютной системы отсчета. В том числе была выдвинута гипотеза о сокращении линейных размеров тел в направлении их движения относительно эфира. При этом Лоренц и Фицджеральд считали, что тела действительно со­кращают свои размеры в направлении движения. Это сокра­щение должно было полностью компенсировать влияние от­носительного движения на скорость распространения света, почему и казалось, что скорость света остается постоянной во всех инерциальных системах отсчета. Несмотря на то, что высказанная гипотеза выглядела очень искусственной и оказалась неверной, как это выяснилось впоследствии, она привела к нахождению уравнений преобразований ки­нематических параметров, отличных от преобразований Га­лилея, которые называют уравнениями Лоренца. При усло­вии, что относительная скорость систем отсчета V велика и сравнима со скоростью света С (V<С), имеем следующее:

24.Постулаты специальной теории относительности. Выводы из анализа преобразований Лоренца

Очевидно, что преобразования Лоренца содержат немыслимые с точки зрения обыденных представлений парадоксы: кроме вышеупо­мянутого сокращения линейных размеров тел, движущихся вместе с системой отсчета K относительно неподвижной системы K:

оказалось, что и длительность событий в этих системах отсчета разная. Если длительность временного интервала в системе K - дельта t, а в системе K' -дельта t', то

Длительность дельта t'- длительность события относительно дви­жущейся системы K', относительно которой тело покоится. Дли­тельность события в системе отсчета, относительно которой тело неподвижно, называется собственным временем. Собственное время дельта t' минимально. Это говорит о том, что относительно системы К ин­тервал времени дельта t оказывается большим. Итак, из преобразований Лоренца следовало, что пространственные и временные интервалы оказываются неинвариантными при переходе из одной системы от­счета в другую. Возникла ситуация, в которой потребовались глубо­кий анализ и критика имеющихся представлений о пространстве и времени, на основании которых удалось бы выяснить причины, по которым преобразования Галилея заменяются преобразованиями Лоренца. Это и было сделано А. Эйнштейном в его вышедшей в свет в 1905 г. работе К электродинамике движущихся сред. Свою статью Эйнштейн начинает с двух предположений, в современной науке именуемых постулатами теории относительности, которые он рассматривает как предпосылки для того, чтобы положив в основу теорию Максвелла для покоящихся тел, построить простую, свобод­ную от противоречий электродинамику движущихся сред. Постулаты теории относительности 1. Принцип относительности: все законы природы одинаковы

во всех инерциальных системах отсчета.

Лоренц отмечал по этому поводу: «Заслуга Эйнштейна состоит в том, что он первый высказал принцип относительности в виде всеобщего, строго и точно действующего закона. Следует отметить, что точки зрения об универсальности принципа относительности придерживался также А. Пуанкаре.

2. Принцип постоянства скорости света: скорость света в пу­стоте одинакова во всех инерциальных системах отсчета и не зависит от движения источников и приемников света.

Исходя из постоянства скорости света, Эйнштейн подвергает критическому анализу традиционное понятие времени. Ньютонов­ское понятие абсолютного, универсального, равномерно текущего времени твердо укоренилось в представлениях физиков и казалось незыблемым. Следствием этого явилось некритически используемое в ньютоновской механике представление об одновременности собы­тий. Критику абсолютного времени Ньютона Эйнштейн начинает с рассмотрения понятия одновременности двух событий, обращая особое внимание на тот факт, «что все наши суждения, в которых время играет какую-либо роль, всегда являются суждениями об одновременных событиях. Установив, что следует понимать под синхронно идущими в разных точках пространства покоящимися часами, Эйнштейн дает определения понятий одновременности и времени. Но установленная таким образом одновременность собы­тий в одной системе отсчета не будет верна в другой, движущейся по отношению к первой. Если один наблюдатель считает одно­временными два события, которые пространственно разобщены, в той системе отсчета, относительно которой он неподвижен, то другой наблюдатель, участвующий в равномерном прямолинейном движении относительно первой системы отсчета, не считает их одновременными. Так что одновременность становится понятием относительным, зависящим от наблюдателя.

Таким образом, следует говорить о собственном времени каждой системы отсчета. Универсальное абсолютное ньютоновское время должно уступить место бесчисленным собственным временам раз­личных систем отсчета. Этот, на первый взгляд, парадоксальный вывод является следствием того, что невозможно синхронизировать часы с помощью сигналов, распространяющихся со скоростью, превышающей скорость света.

Наше же обыденное представление о времени, совпадающее с представлением об универсальном ньютоновском времени, - след­ствие того, что мы живем в мире малых скоростей, неосознанно пользуясь при этом информационными волнами, распространяющимися со скоростями, сравнимыми со скоростью света. Если бы скорость электромагнитных волн была бы порядка обычных для нашего сознания скоростей, то гораздо раньше встал бы вопрос об одновременности событий в различных точках пространства. Эйнштейн показал, что в основе преобразований Галилея как раз и лежит произвольное допущение о том, что понятие одновременно­сти имеет смысл независимо от состояния движения используемой системы координат.

Рассуждая таким образом и используя два указанных выше принципа (постулаты теории относительности), Эйнштейн мате­матически вывел Лоренцево сокращение движущихся тел K при их наблюдении из покоящейся системы, при условии, что ско­рость движущегося тела V=С. Следствием Лоренцева сокращения является эффект замедления времени. То же обстоятельство, что длительности событий различны в различных системах отсчета, приводит к замене Галилеева правила сложения скоростей реля­тивистским законом сложения скоростей. Из релятивистского закона сложения скоростей следует, что сложение скорости света со скоростью источника дает во всех случаях опять-таки скорость света, тем самым скорость света в пустоте - максимальная скорость передачи взаимодействий в природе.

Таким образом, изменение понятий о пространстве и времени приводит в специальной теории относительности к изменению основных принципов кинематики. Новая кинематика, к которой пришел Эйнштейн при анализе понятий пространства и времени, со­впала с преобразованиями, полученными ранее Лоренцем. Однако Эйнштейн наполняет преобразования Лоренца новым физическим содержанием. Так, если Лоренц рассматривал сокращение линей­ных размеров движущихся тел как действительное сокращение по отношению к неподвижному эфиру, то Эйнштейн рассматривает это сокращение как кажущееся для наблюдателя, относительно которого тело движется. Сокращение линейных размеров тел и замедление длительности временных интервалов - это следствие различных процессов измерения, которыми пользуются различные наблюдатели в различных системах отсчета.

Итак, два постулата принципа относительности должны быть дополнены преобразованиями Лоренца. Чтобы принцип относи­тельности мог выполняться, необходимо, чтобы все законы физики не изменяли своего вида, были инвариантны при переходе из одной инерциальной системы отсчета в другую относительно преобразо­ваний Лоренца. Это одно из первых следствий, вытекающих из постулатов теории относительности, устанавливающее критерий включения физического закона в релятивистскую схему. Эйнштейн показал также, что преобразования Лоренца переходят в преоб­разования Галилея при скоростях V<<С, тем самым устанавливая границы применимости классической механики для мира малых скоростей.

25. Содержание трансдисциплинарных концепций релятивистской исследовательской программы

Преобразования Галилея основывались на гипотезе о полной независимости времени и пространства. Это приводило к тому, что пространственные и временные интервалы рассматривались по отдельности неизменными при переходе из одной системы отсчета в другую. То есть двум соседним точкам пространства ставилась в соответствие численная мера dS, выражаемая уравнением

не зависит от выбора системы координат и может быть из­мерена единичным измерительным стержнем.

Независимо от этого двум событиям ставился в соответствие временной интервал dt, также не зависящий от системы отсчета. Однако специальная теория относительности в корне изменяет сложившийся взгляд.

Из самого вида преобразований Лоренца отчетливо видно, что пространственные и временные координаты больше не могут быть рассмотрены независимо. Г. Минковский, исходя из положения, что пространство и время - понятия, неотделимые друг от друга, предложил математический формализм, запись в котором физи­ческого закона приводит к его инвариантности относительно пре­образований Лоренца.

Формализм Минковского использует представление о четы­рехмерном мире, четырехмерном пространственно-временном кон­тинууме, в котором время по своему месту в физических уравнениях эквивалентно трем пространственным координатам.

Двум соседним точкам в четырехмерном пространстве-времени ставится в соответствие численная мера, называемая мировым интервалом и выражаемая уравнением:

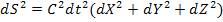
Именно мировой интервал не зависит от выбора системы отсчета, остается инвариантным относительно преобразований Лоренца. Каждый наблюдатель, находящийся в своей инерциальной системе отсчета, по-своему отделяет пространство и время из четырехмер­ного пространственно-временного мира, но мировой интервал dS остается для каждого из них неизменным.

Специальная теория относительности - теория, которая решает две основные задачи: во-первых, приспосабливает пространственно-временную метрику к уравнениям Максвелла. Это приводит к выработке новой метрики пространства-времени, где на смену евклидовой метрике, в которой пространство и время рассматрива­ются независимыми друг от друга и в которой пространственные и временные масштабы сохраняют неизменность по отдельности друг от друга в различных системах отсчета, приходит видоизмененная метрика с пространственно-временным континуумом, называемым псевдоевклидовым пространством Минковского, в котором время эквивалентно пространственным координатам, играет роль чет­вертого измерения в этом континууме и в котором инвариантным относительно преобразований Лоренца является четырехмерный мировой интервал. И, во-вторых, применение этой новой метри­ки ко всей физике. Этот второй этап приводит к видоизменению ньютоновских законов движения на случай больших скоростей и к закону взаимосвязи массы тела и энергии Е = mc*2.

В дальнейшем все известные физические законы были записаны в четырехмерном формализме Минковского, что привело к созда­нию новой релятивистской (relativ - относительный) физической исследовательской программы, пришедшей на смену механисти­ческой исследовательской программе.

Трансдисциплинарные концепции релятивистской иссле­довательской программы:

1. Концепция относительности (инвариантности).

2. Концепция микропричинности, согласно которой взаи­модействия передаются с конечной скоростью, равной ско­рости света.

3. Концепция единого четырехмерного пространственно-вре­менного континуума.

26. Мотивы создания общей теории относительности. Концепция инвариантности как трансдисциплинарная идея естествознания

Благодаря специальной теории относительности в физике создается новый взгляд на характер физических законов, «наи­совершеннейшим выражением которых считается теперь их инва­риантное выражение о. Несмотря на революционность специальной теории относительности, приведшей к коренному изменению наших представлений о пространстве и времени, тем не менее возникает чувство некоторой незавершенности теории. И связано это с тем, что специальная теория относительности, так же как и классическая механика, сохраняет привилегированное положение наблюдателей, находящихся в инерциальных системах отсчета. А как быть с на­блюдателями, находящимися в системах отсчета, движущихся по отношению к первым с ускорением (в неинерци-альных системах отсчета)? Чем объясняется неинвариантность законов физики в неинерциальных системах отсчета? Правомерно ли это? Подобное положение дел казалось неудовлетворительным. Эйнштейн, по­вторяя вопрос Э. Маха: Почему инерциальные системы физически выделены относительно других систем отсчета? - первым обращает внимание на то, что специальная теория относительности не дает на него ответа. Следующая проблема возникла при попытке представить в рамках СТО тяготение. Оказалось, что тяготение укладывается в рамки специальной теории относительности только в том случае, если потенциал гравитационного поля постоянен. Эйнштейном была выяснена причина этого: она состоит в том, что не только инертная масса зависит от энергии, но и гравитационная. Галилеем был уста­новлен закон, согласно которому все тела падают, при отсутствии сопротивления среды, с одинаковым ускорением. Это является следствием равенства инертной и гравитационной (весомой) массы. Равенство инертной и гравитационной массы соблюдается с точнос­тью выше одной двадцатимиллионной, что было показано в серии весьма точных опытов, проделанных Р. Этвешем. Тем не менее это равенство не получило объяснения в физической теории. В 1908 г. Эйнштейн доказывает, что каждому количеству энергии в гравита­ционном поле соответствует энергия, по величине равная энергии инертной массы величиной E/с*2, и делает вывод о том, что закон этот выполняется не только для инертной, но и для гравитационной массы. Рассматривая факт равенства инертной и гравитационной массы, Эйнштейн приходит к выводу о том, что гравитационное поле (в котором проявляется гравитационная масса) эквивалентно уско­ренному движению (в котором проявляется масса инертная) и форму­лирует принцип эквивалентности, который и был положен в основу создания общей теории относительности: «Факт равенства инертной и весомой массы, или, иначе, тот факт, что ускорение свободного падения не зависит от природы падающего вещества, допускает и иное выражение. Его можно выразить так: в поле тяготения (малой пространственной протяженности) все происходит так, как в про­странстве без тяготения, если в нем вместо «инерциальной» системы отсчета ввести систему, ускоренную относительно нее. Эйнштейн приходит к выводу о том, что главная задача состоит не в том, как включить тяготение в СТО, а в том, как использовать тяготение для обобщения требования инвариантности к любым типам движения, в том числе и ускоренным. Оказалось, что тяготение не может быть полностью заменено ускорением (гравитационные силы — силами инерции) в больших областях с неоднородным гравитационным полем. Сведение гравитационного поля к ускоренным системам от­счета требует ограничения принципа эквивалентности бесконечно малыми масштабами. Иными словами, принцип эквивалентности имеет локальное значение.

Локальный характер принципа эквивалентности приводит к пред­ставлениям о мире, отличном от плоского Евклидова пространства, для которого сумма углов треугольника всегда равна 180°. Это мир с кривизной пространственно-временного континуума. Случилось так, что в математике уже были развиты теории Неевклидовой дифферен­циальной геометрии - теория Лобачевского и теория Римана. В общей теории относительности инвариантность физических законов в систе­мах отсчета, в которых действуют гравитационные силы (или которые являются неинерциальными), достигается относительно локальных преобразований в римановом четырехмерном пространстве-времени положительной кривизны. Иными словами, гравитационное поле мо­жет интерпретироваться как следствие искривления пространства.

Дата добавления: 2014-12-07