Лекция №7

Построить тени от прямой DE и треугольника АВС, падающие на плоскость π1. Построить тени от прямой на плоскость треугольника АВС

В задаче видно, что все координаты точек z больше, чем y, а это значит что тень от треугольника и от прямой ED упадет на горизонтальную плоскость. Следовательно, можно строить только действительные тени каждой точки.

Строим действительные тени точек А1 В1С1 Е1. Соединяем тени точек треугольника Ап1 Вп1 Сп1 между собой и тень от прямой Dп1 Еп1 пересекает тень от треугольника в точках 1п1 и 2п1. Это значит, что прямая DЕ будет отбрасывать тень на проекции треугольника.

Проецируем точки 1п1 и 2п1 обратным лучом на проекцию Δ А1В1С1.

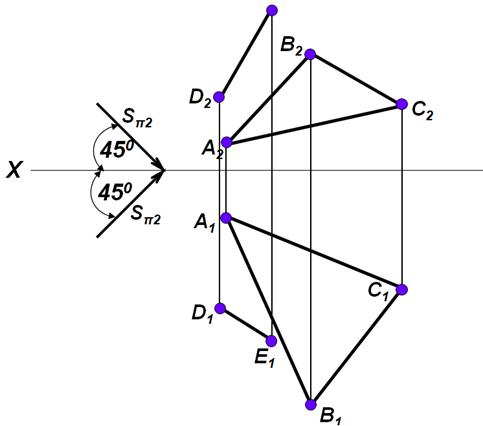
Соединяем точки 11 и 21, получим горизонтальную проекцию тени на проекции треугольника.

Проецируем точки 1 и 2 на фронтальную проекцию сторон треугольника. 12 22 – это тень на фронтальной проекции треугольника.

Построить тень от призмы

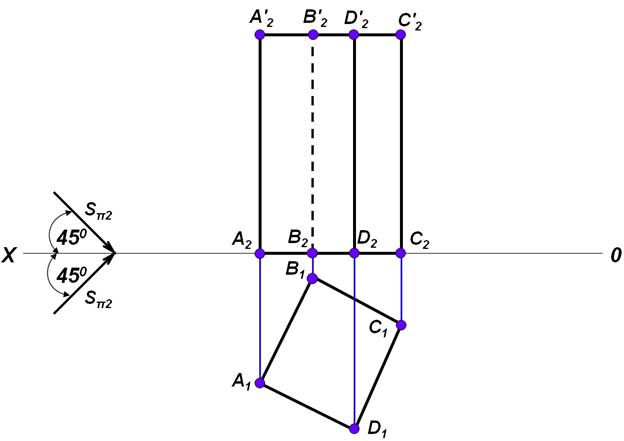
Верхнее основание призмы отстоит от оси х на большую величину, чем на горизонтальной плоскости, а это значит, что тень от точек верхнего основания упадет на плоскость П2.

А тень от точек нижнего основания совпадет с проекциями точек нижнего основания. Значит, каждое ребро призмы на горизонтальной плоскости отбросит тень по направлению светового луча, а на фронтальной проекции с направлением преломленного горизонтального луча.

Строим тень от всех точек верхнего основания. Ап2; Вп2; Сп2; Dп2.

Соединяем эти точки между собой: А2В2 - штриховой линией, т.к. находится за фигурой призмы.

В2С2 частично штриховой, остальное контурной линией. А2D2 попадают в зону тени, поэтому также соединяем их штриховой линией.

Обводим видимую границу тени контурной линией и штрихуем падающую тень. Собственная тень – это неосвещенная грань D2С2С '2 D '2.

Построить тень от пирамиды

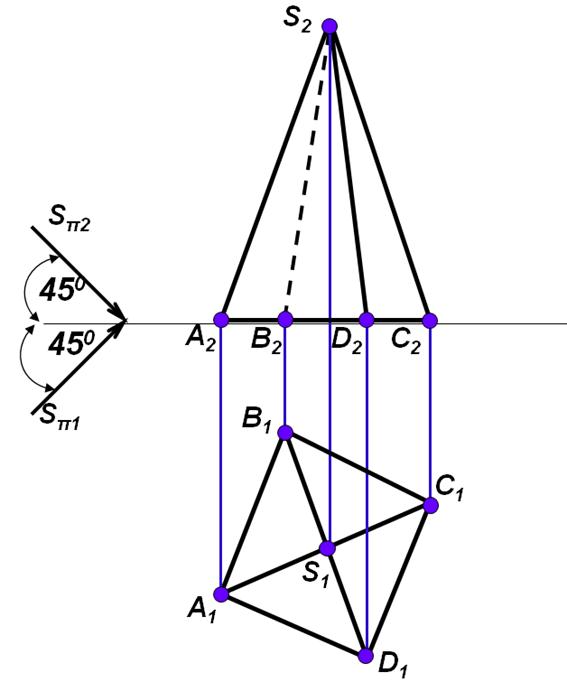
Строим действительную и мнимую тени от вершины пирамиды (Sп1)Sп2. Тень от точек основания совпадает со своими проекциями, т.е. В1 ≡ Вп1 D1 ≡ Dп1.

Соединяем одноименные тени точек ВD и S → Вп1Sп1 Dп1 – это тень на горизонтальной плоскости проекций. Но эта тень пересекает ось х, а значит преломляется в точках 11≡2 и 21≡2.

Соединяем эти точки с Sп2, получаем действительную тень 12Sп2 22 на фронтальной плоскости проекций. Обводим действительную тень на обе плоскости проекций и отмываем.

Собственная тень ограничена на горизонтальной проекции ребрами D1S1 и S1В1, а на фронтальной плоскости проекций видимая собственная тень ограничена ребром S2 D2.

Построить тень от конуса

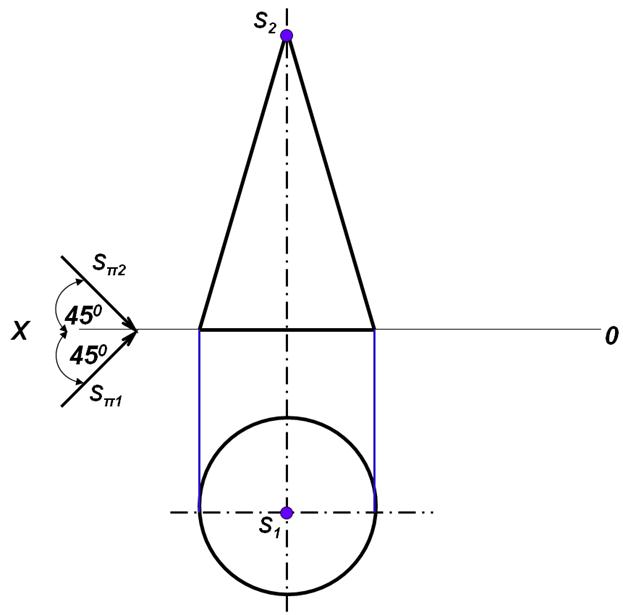
Для построения падающей тени конуса необходимо построить тень от вершины S [Sп2 (Sп1)]. Проводим из точки Sп1 касательно к окружности основания границу тени на плоскость П1.

Полученная тень будет преломляться на оси х в точках 11 и 21. Соединяем эти точки с Sп2. 11 Sп221 – это тень от конуса на плоскость П2.

Строим собственную тень конуса. Опускаем из точки S1 перпендикуляры к границам падающей тени на горизонтальную плоскость. Обозначим полученные точки 31 и 41. На горизонтальной проекции собственная тень – это сектор, ограниченный радиусами S31 и S41.

Переносим точки 3 и 4 на фронтальную проекцию и соединяем с вершиной S2. Образующая 42 S2 является видимой границей света и тенью на фронтальной плоскости проекций, а образующая 32 S2 является невидимой границей, поэтому проводится штриховой линией.

Построить тень в нише здания

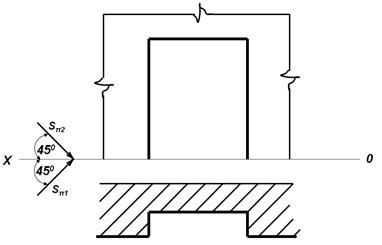
Начинаем с горизонтальной проекции. Горизонтальный луч, проведенный из точки 11 под 45°,соприкасаясь со стеной, преломляется на фронтальной проекции по вертикальной прямой до пересечения с фронтальным лучом, проведенным из точки 12. Полученная точка - тень от 1п2 - это тень от точки 1. Тень от потолка ниши пройдет через точку 1п2 параллельно потолку, а от ребра1 по преломленному лучу.

Построить тень от выступающей плиты на фасаде

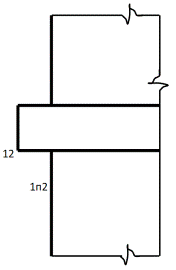
Из нижней левой точки плиты 12 проводим фронтальный световой луч до фасада. Тень будет проходить параллельно плиты через точку 1п2, которая определяется пересечением фронтального луча, проведенного под 450 из точки плиты 12.

Построить тень от козырька на фасаде здания и в нише

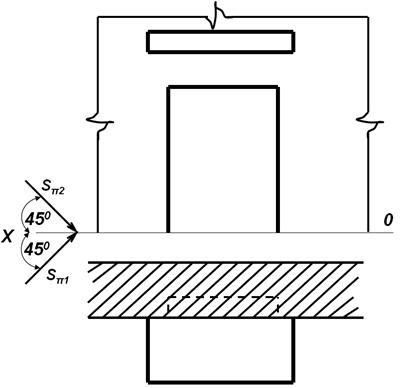
Чтобы построить тень от козырька обозначимна козырьке только те точки, которые отбросят тень: 11; 21; 31;41;12;22;32;42. Начинаем построение из точек 21 ≡31 Проводим горизонтальный световой луч из этой точки до фасада, луч преломляется и на фронтальной проекции, располагается вертикально, до пересечения с фронтальными световыми лучами, проведенными из точек 22; 32. На пересечении найдем тень от этих точек 2п2; 3п2. Тень от нижней грани козырька отбросит тень, проходящую через точку 2п2 параллельно грани козырька и закончится слева в точке 1п2, которая находится так же, как 2п2. Соединяем 5 точек (12;1п2;2п2;3п2 и 4п2). Это тень от козырька на фасаде. Козырек отбросит тень и в нишу. Построение этой тени нужно начать с точки 11. Световой луч продолжаем до точки в нише. Преломленный луч поднимается вертикально вверх до пересечения с фронтальным лучом из точки 12. Тень от этой точки обозначаем 1 'п2. Соединяем 12 и 1 'п2. Тень от горизонтального участка козырька пройдет через точку 1 'п2 параллельно горизонтальной поверхности козырька.

Построить тени на ступенях

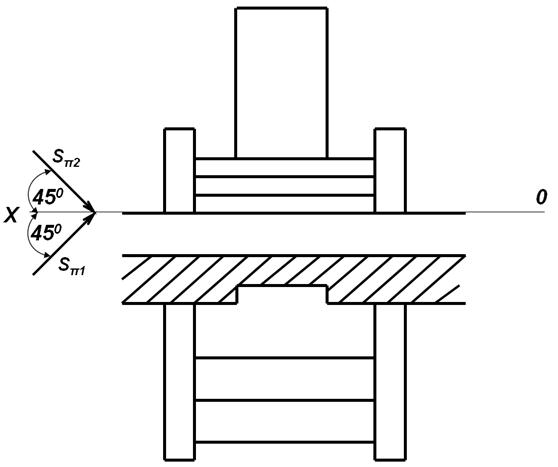
Тень от ограждения ступенек начинаем строить с фронтальной проекции от точки 12. Проводим фронтальный луч из точки 12. Точку пересечения луча с площадкой проецируем на горизонтальную проекцию площадки. Пересечение луча со второй ступенькой проецируем на горизонтальную проекцию второй ступеньки. Горизонтальный световой луч, преломившись на 1-ой ступеньке, отбрасывает тень на 1-ую ступеньку фронтальной проекции. Пересекаясь со второй ступенькой, отбрасывает на вторую, но уже не на всю высоту, так как встречается с фронтальным лучом. Тень от правого ограждения отбрасывается на землю и фасад здания. Построения показаны стрелкой.

ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА

Брилинг Н.С. Черчение. М., Стройиздат. 1982.470с. с ил.

Г.В. Серга, С.Г. Кочубей, Н.К. Кузнецова. Курс инженерной графики ч.1. Краснодар, КубГАУ, 2009.

Г.В. Серга, С.Г. Кочубей, Н.К. Кузнецова, И.И. Табачук. Курс инженерной графики ч.2. Краснодар, КубГАУ, 2009.

Сербина Е.И. Сборник задач по начертательной геометрии. М., «Высшая школа», 1984, 220с. с ил.

Крылов Н.Н. Начертательная геометрия. М., «Высшая школа», 1984. 220с.

Бубенников А.В. Начертательная геометрия. М., «Высшая школа», 1985. 287 с. с ил.

Гордон В.О. Курс начертательной геометрии. М., «Наука», 1981 и другие издания.

Дата добавления: 2014-12-07