КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вопросы по главе. 1. Что понимается под множественной регрессией?
|
|
|
|
1. Что понимается под множественной регрессией?
2. Какие задачи решаются при построении уравнения регрессии?
3. Какие задачи решаются при спецификации модели?
4. Какие требования предъявляются к факторам, включаемым в уравнение регрессии?
5. Что понимается под коллинеарностью и мультиколлинеарностью факторов?
6. Как проверяется наличие коллинеарности и мультиколлинеарности?
7. Какие подходы применяются для преодоления межфакторной корреляции?
8. Какой вид имеет система нормальных уравнений метода наименьших квадратов в случае линейной регрессии?
9. По какой формуле вычисляется индекс множественной корреляции?
10. Как вычисляются индекс множественной детерминации и скорректированный индекс множественной детерминации?
11. Что означает низкое значение коэффициента (индекса) множественной корреляции?
12. Как проверяется значимость уравнения регрессии и отдельных коэффициентов?
13. Как строятся частные уравнения регрессии?
14. Как вычисляются средние частные коэффициенты эластичности?
15. Что такое стандартизированные переменные?
16. Какой вид имеет уравнение линейной регрессии в стандартизированном масштабе?
17. Как оценивается информативность (значимость) факторов?
18. Как вычисляются частные коэффициенты корреляции?
19. Опишите процедуру метода исключения переменных с использованием частных коэффициентов корреляции.
20. Что понимается под гомоскедастичностью?
21. Как проверяется гипотеза о гомоскедастичности ряда остатков?
22. В чем суть метода Гольдфельда – Квандта и для чего он применяется?
Задание №3. Модель множественной линейной регрессии.
Имеются данные по 20 квартирам (таб. 1).
Таблица 1
| № | Кол-во комнат | Район | План. | Материал стен | Этаж | Этаж-ность | Sоб | Sжил | Sкух | Тел. | Санузел | Балкон/ лоджия | Плита | Цена |
| 4,00 | 13,00 | 5,00 | 1,00 | 1,00 | 9,00 | 82,00 | 51,00 | 9,00 | 1,00 | 3,00 | 1,00 | 1,00 | 3500,00 | |
| 3,00 | 10,00 | 5,00 | 2,00 | 6,00 | 9,00 | 64,00 | 40,00 | 9,00 | 1,00 | 3,00 | 3,00 | 1,00 | 3400,00 | |
| 4,00 | 11,00 | 5,00 | 1,00 | 8,00 | 10,00 | 83,00 | 50,00 | 9,00 | 1,00 | 3,00 | 2,00 | 3,00 | 4000,00 | |
| 3,00 | 8,00 | 3,00 | 1,00 | 5,00 | 5,00 | 61,00 | 45,00 | 6,00 | 1,00 | 3,00 | 2,00 | 3,00 | 2500,00 | |
| 3,00 | 10,00 | 5,00 | 2,00 | 3,00 | 5,00 | 120,00 | 80,00 | 12,00 | 2,00 | 1,00 | 2,00 | 3,00 | 5800,00 | |
| 3,00 | 10,00 | 2,00 | 1,00 | 2,00 | 5,00 | 63,00 | 40,00 | 8,00 | 1,00 | 3,00 | 3,00 | 3,00 | 2000,00 | |
| 5,00 | 42,00 | 5,00 | 1,00 | 4,00 | 9,00 | 98,00 | 65,00 | 9,00 | 1,00 | 1,00 | 1,00 | 3,00 | 3000,00 | |
| 4,00 | 13,00 | 5,00 | 1,00 | 1,00 | 9,00 | 82,00 | 50,00 | 9,00 | 1,00 | 3,00 | 2,00 | 3,00 | 3200,00 | |
| 4,00 | 15,00 | 3,00 | 1,00 | 4,00 | 5,00 | 64,00 | 43,00 | 7,00 | 1,00 | 1,00 | 1,00 | 3,00 | 2600,00 | |
| 1,00 | 3,00 | 1,00 | 1,00 | 1,00 | 5,00 | 42,00 | 18,00 | 9,00 | 1,00 | 3,00 | 2,00 | 3,00 | 1650,00 | |
| 4,00 | 15,00 | 3,00 | 1,00 | 1,00 | 5,00 | 62,00 | 48,00 | 6,00 | 1,00 | 2,00 | 1,00 | 2,00 | 2300,00 | |
| 3,00 | 8,00 | 3,00 | 1,00 | 3,00 | 5,00 | 48,00 | 26,00 | 7,00 | 2,00 | 3,00 | 2,00 | 2,00 | 2500,00 | |
| 3,00 | 8,00 | 3,00 | 2,00 | 2,00 | 5,00 | 63,00 | 48,00 | 6,00 | 1,00 | 3,00 | 2,00 | 3,00 | 2100,00 | |
| 3,00 | 9,00 | 2,00 | 1,00 | 1,00 | 5,00 | 63,00 | 40,00 | 9,00 | 1,00 | 3,00 | 3,00 | 3,00 | 1600,00 | |
| 3,00 | 9,00 | 5,00 | 1,00 | 6,00 | 10,00 | 68,00 | 40,00 | 12,00 | 1,00 | 3,00 | 2,00 | 3,00 | 1650,00 | |
| 3,00 | 10,00 | 5,00 | 1,00 | 2,00 | 9,00 | 64,00 | 40,00 | 9,00 | 2,00 | 2,00 | 2,00 | 3,00 | 3000,00 | |
| 4,00 | 13,00 | 5,00 | 1,00 | 2,00 | 9,00 | 82,00 | 50,00 | 9,00 | 1,00 | 3,00 | 4,00 | 3,00 | 2800,00 | |
| 4,00 | 11,00 | 5,00 | 1,00 | 10,00 | 10,00 | 81,00 | 50,00 | 12,00 | 1,00 | 1,00 | 4,00 | 1,00 | 3600,00 | |
| 5,00 | 51,00 | 5,00 | 1,00 | 4,00 | 9,00 | 99,00 | 65,00 | 9,00 | 1,00 | 3,00 | 4,00 | 3,00 | 2500,00 | |
| 3,00 | 8,00 | 3,00 | 1,00 | 2,00 | 5,00 | 62,00 | 45,00 | 7,00 | 1,00 | 2,00 | 2,00 | 2,00 | 2800,00 | |
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | x11 | x12 | x13 | y |
Задания:
1. Рассчитайте параметры линейного уравнения множественной регрессии с полным перечнем факторов двумя способами.
2. Оцените качество уравнения регрессии при помощи коэффициентов детерминации. Проверьте нулевую гипотезу о значимости уравнения и показателей тесноты связи с помощью F-критерия Фишера.
3. Дайте сравнительную оценку силы влияния факторов с результатом с помощью стандартизированных коэффициентов регрессии.
4. Рассчитайте матрицы парных коэффициентов корреляции. Прокомментируйте полученные результаты.
5. На основе полученных показателей отберите существенные факторы в модель. Постройте модель только с существенными переменными и оцените ее параметры. Оцените статистическую значимость параметров «укороченного» уравнения регрессии, а также оцените его качество в целом. Сравните ее с предыдущей регрессионной моделью.
6. Для построения модели используйте метод всех регрессий.
Решение
1. Линейная модель множественной регрессии имеет вид:
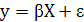, (1)
где для имеющихся данных
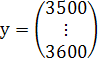– вектор объясняемых переменных,
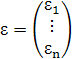– вектор ошибок,
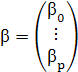– вектор коэффициентов,
– матрица объясняющих переменных.
Для получения уравнения регрессии используем Метод Наименьших Квадратов.
Найдем вектор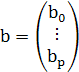 
– вектор, оценивающий коэффициенты 
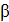, чтобы определить 
– вектор расчетных значений объясняемых переменных при заданных коэффициентах.
В Excel это можно организовать с помощью функции Поиск Решений
(для подключения этого инструмента в программном продукте MS Office Exсel 2007 необходимо выполнить следующее:
1. Щелкните значок Кнопка Настройка панели быстрого доступа 
, а затем щелкните Другие команды.
2. Выберите команду Надстройки, а затем в окне Управление выберите пункт Надстройки Excel.
3. Нажмите кнопку Перейти.
4. В окне Доступные надстройки установите флажок Поиск решения и нажмите кнопку ОК.
Совет Если Поиск решения отсутствует в списке поля Доступные надстройки, чтобы найти надстройку, нажмите кнопку Обзор.
В случае появления сообщения о том, что надстройка для поиска решения не установлена на компьютере, нажмите кнопку Да, чтобы установить ее.
5. После загрузки надстройки для поиска решения в группе Анализ на вкладки Данные становится доступна команда Поиск решения.)
Создадим таблицу коэффициентов (Таблица 2), придав им случайные значения (количество коэффициентов равно количеству переменных Х плюс коэффициент b0 – свободный член):
Таблица 2.
|
|
|
|
|
Дата добавления: 2014-12-07; Просмотров: 1165; Нарушение авторских прав?; Мы поможем в написании вашей работы!