Регрессионная статистика

Оценка качества уравнения регрессии при помощи коэффициентов детерминации. Проверка нулевой гипотезы о значимости уравнения и показателей тесноты связи с помощью F-критерия Фишера.

Стандартные ошибки коэффициентов.

	Стандартная ошибка
Свободный член	1304,48
Количество комнат	226,77
Район	10,31
Планировка	277,57
Материал стен	287,54
Этаж	35,31
Этажность	150,93
Sоб	22,35
Sжил	31,19
Sкух	97,68
Телефон	331,79
Санузел	127,84
Балкон/лоджия	86,06
Плита	105,08

Уравнение регрессии имеет вид:

Y	=3378,41	-494,59X1	-35,00X2	+75,74X3	-15,81X4	+80,10X5	+59,84X6 +
	(1304,48)	(226,77)	(10,31)	(277,57)	(287,54)	(35,31)	(150,93)

+127,98X7	-78,10X8	-437,57X9	+451,26X10	-299,91X11	-14,93X12	-369,65X13	(9)
(22,35)	(31,19)	(97,68)	(331,79)	(127,84)	86,06	(105,08)

Для заполнения таблицы «Регрессионная статистика» (Таблица 9) находим:

1. Множественный R – r-коэффициент корреляции между у и ŷ.

Для этого следует воспользоваться функцией КОРРЕЛ, введя массивы у и ŷ.

Полученное в результате число 0,99 близко к 1, что показывает очень сильную связь между опытными данными и расчетными.

2. Для расчета R-квадрат находим:

Объясняемая ошибка 17455259,48,

.

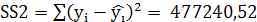Необъясняемая ошибка .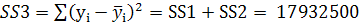

Следовательно, R-квадрат равен .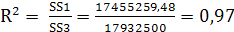

Соответственно 97% опытных данных объяснимы полученным уравнением регрессии.

3. Нормированный R-квадрат находим по формуле

.

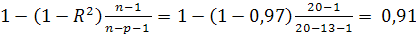Этот показатель служит для сравнения разных моделей регрессии при изменении состава объясняющих переменных.

4. Стандартная ошибка – квадратный корень из выборочной остаточной дисперсии:

.

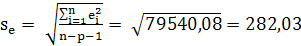В результате получаем следующую таблицу.

Таблица 9.

Множественный R	0,99
R-квадрат	0,97
Нормированный R-квадрат	0,92
Стандартная ошибка	282,03
Наблюдения	20,00

Заполнение таблицы «Дисперсионный анализ»

Большая часть данных уже получена выше. (Объясняемая и необъясняемая ошибка).

Рассчитаем t wx:val="Cambria Math"/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>13</m:t></m:r></m:den></m:f><m:r><m:rPr><m:sty m:val="p"/></m:rPr><w:rPr><w:rFonts w:ascii="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t> = 1342712,27</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> .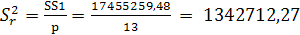

Оценку статистической значимости уравнения регрессии в целом проведем с помощью F -критерия Фишера. Уравнение множественной регрессии значимо (иначе – гипотеза H₀ о равенстве нулю параметров регрессионной модели, т.е. 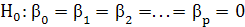отвергается), если

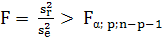, (10)

где 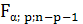- табличное значение F-критерия Фишера.

Фактическое значение F - критерия по формуле составит:

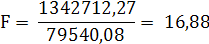
Для расчета табличного значения критерия Фишера используется функция FРАСПОБР (Рисунок 4).

Степень свободы 1: p=13

Степень свободы 2: n-p-1 = 20-13-1=6

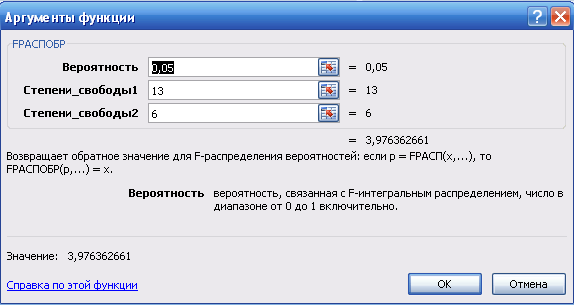
Рисунок 4. Использование функции FРАСПОБР в Excel.

F_табл = 3,976 < 16,88, следовательно, модель адекватна опытным данным.

Значимость F рассчитывается с помощью функции FРАСП. Эта функция возвращает F-распределение вероятности (распределение Фишера) и позволяет определить, имеют ли два множества данных различные степени разброса результатов.

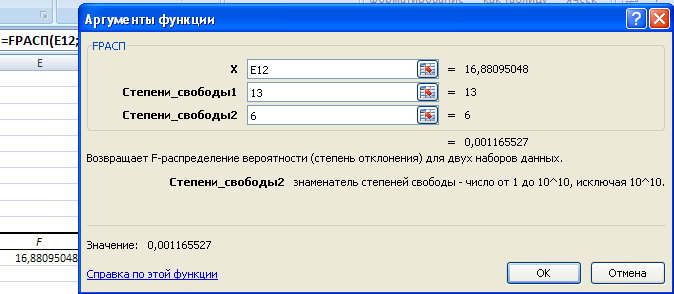
Рисунок 5. Использование функции FРАСП в Excel.

Значимость F = 0,001.

Таблица 10.

Дата добавления: 2014-12-07