Краткие сведения о межотраслевом балансе

Исследование модели межотраслевого баланса

Лабораторная работа № 3

Библиографический список

Содержание отчета

4.1. Модели Солоу в базовом и расширенном вариантах. Графическое представление базовой модели.

4.2. Программы и графики, необходимые для получения результатов.

4.3. Результаты экспериментов.

4.4. Выводы по работе.

1. Ашманов С.А. Введение в математическую экономику. М.: Наука, 1984. 296 с.

2. Мэнкью Н.Г. Макроэкономика. М.: МГУ, 1994. 736 с.

Цель работы: планирование выпуска продукции и исследование межотраслевого баланса.

Межотраслевой баланс (МОБ) представляет собой таблицу, характеризующую связи между n отраслями (экономическими объектами) экономической системы (другими словами, таблица характеризует межотраслевые потоки товаров и услуг в течение фиксированного периода времени – года).

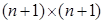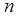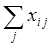МОБ состоит из четырех квадрантов. Первый квадрант представляет таблицу из ячеек. Первые ячеек каждой строки содержат объемы поставок продукта i -й отрасли другим отраслям . Сумма этих поставок выражает суммарное производственное потребление продукта i -й отрасли и записывается в i -й строке (n +1)-го столбца МОБ. В 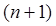-й строке каждого столбца записана сумма текущих производственных затрат i -й отрасли за год 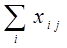. Величина 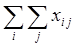представляет собой промежуточный продукт экономической системы.

Второй квадрант МОБ расположен справа от первого и состоит из двух столбцов: конечного 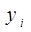и валового 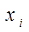продуктов отраслей. Суммарный (валовой) выпуск i -й отрасли равен

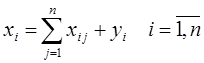. (3.1)

Соотношения (3.1) принято называть балансом распределения продукции, который показывает, что вся произведенная i -й отраслью продукция 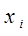потребляется. Часть ее в форме 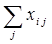суммарного производственного потребления идет на производственные нужды отраслей экономики. Другая часть потребляется в форме конечного продукта .

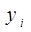Третий квадрант расположен в таблице под первым квадрантом и состоит из двух строк, одна из которых отражает объем валового продукта по отраслям, а другая строка – условно чистый продукт (валовую добавленную стоимость) отраслей .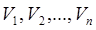

Валовая добавленная стоимость представляет разность между валовым продуктом отрасли и суммой ее текущих производственных затрат

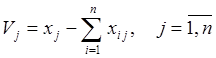. (3.2)

Введем в рассмотрение вектор валового выпуска системы 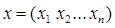, вектор конечного продукта 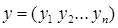и матрицу прямых затрат 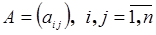. Коэффициенты прямых затрат (технологические коэффициенты) 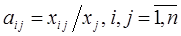, показывают объем продукта 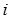- й отрасли, израсходованного на производство одной единицы продукта 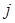- й отрасли. Тогда систему (3.1) можно записать в векторной форме, дополнив ее условием неотрицательности введенных векторов, что обусловлено экономическим смыслом задачи

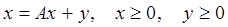. (3.3)

Соотношения (3.3) называют моделью «Затраты – выпуск» или статической моделью Леонтьева.

Основная задача, возникающая при краткосрочном планировании производства: при заданном конечном продукте 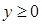требуется определить необходимый выпуск валового продукта 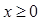, т.е. ответить на вопрос, любой ли конечный спрос может быть удовлетворен при существующей технологии производства. Когда решение системы (3.3) существует для 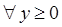, говорят, что модель Леонтьева (и матрица А) продуктивна.

Модель Леонтьева (3.3) продуктивна тогда и только тогда, когда главное собственное число 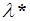матрицы прямых затрат меньше единицы, т.е. .

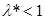Дата добавления: 2014-12-07