Статика. Теоретический материал лекции №1-4

Теоретический материал лекции №1-4

КРАТКИЙ КОНСПЕКТ ЛЕКЦИЙ

Лекция 14-15

1. В чем заключается явление потери устойчивости сжатого стержня.
2. Какая сила называется критической.
3. Как определяется критическая сила.
4. Что такое гибкость стержня.
5. Что такое приведенная длина стержня.
6. Какова область применения формулы Эйлера.
7. В каких случаях применяется формула Ясинского.
8. Какие виды расчета на устойчивость существуют.
9. Что такое коэффициент продольного изгиба j.
10. как производится проверка стержня на устойчивость с помощью коэффициента j.

Теоретическая механика занимается изучением самой простой формы движения материального мира, изучением перемещения тел относительно друг друга во взаимодействии друг с другом. Такое перемещение называется механическим движением. Теоретическая механика разделяется на три части: статику, кинематику и динамику.

Статика – раздел теоретической механики, занимающийся изучением сил и условий их равновесия.

Объектом изучения теоретической механики служат не реально существующие тела, а наделенные идеальными свойствами их абстрактные образы (модели) – материальная точка и абсолютно твёрдое тело (АТТ).

Материальной точкой называют тело, размерами которого в данной задаче можно пренебречь.

АТТ (Абсолютно твердое тело) - это тело, расстояние между двумя любыми точками которого неизменно.

Сила – мера механического воздействия одного тела на другое; она характеризуется модулем, точкой приложения, направлением. Сила – вектор; измеряется в ньютонах (Н).

Система сил – несколько сил, действующих на одно тело. Если действие систем одинаково, они называются эквивалентными. Сила, эквивалентная данной системе сил, называется равнодействующей. Силы делятся на внешние и внутренние.

Статика занимается задачами сложения и разложения сил. Они решаются на основе нескольких аксиом:

I. Всякая изолированная материальная точка находиться в состоянии покоя или равномерного прямолинейного движения, пока приложенные силы не выведут её из этого состояния.

II. Две силы, приложенные к твердому телу, образуют уравновешенную систему тогда и только тогда, когда они равны по модулю и действуют вдоль одной прямой в противоположные стороны.

III. Действие данной системы сил на твердое тело не измениться, если к ней добавить или от нее отнять уравновешенную систему сил.

Следствие 1. Силу, приложенную к твердому телу, можно переносить вдоль линии её действия в любую другую точку, действие силы на тело при этом не изменится.

IV. Две приложенные к точке тела силы имеют равнодействующую, приложенную в той же точке и равную диагонали параллелограмма, построенного на этих силах, как на сторонах (аналогично, правило треугольника).

Следствие 2. Если три непараллельные силы, лежащие в одной плоскости, образуют уравновешенную систему, то линии действия этих сил пересекаются в одной точке.

V. Силы взаимодействия двух твердых тел равны по модулю и направлены по одной прямой в противоположные стороны.

VI. Если деформируемое тело находиться в равновесии, то равновесие этого тела не нарушается, если не изменяя формы, размеров, положения в пространстве, оно превратиться в абсолютно твёрдое тело, т.е. затвердеет.

Твердое тело называется свободным, если оно может перемещаться в пространстве в любом направлении (например, воздушный шар). Твердое тело называется несвободным, если его перемещение в пространстве ограничено какими-либо телами, т.е. его связями. Действие связи на тело называется силой реакции связи или реакцией связи.

Виды связей (рис. 1):

1) свободное опирание;

2) гибкая связь;

3) стержневая связь;

4) шарнирно-подвижная опора;

5) шарнирно-неподвижная опора.

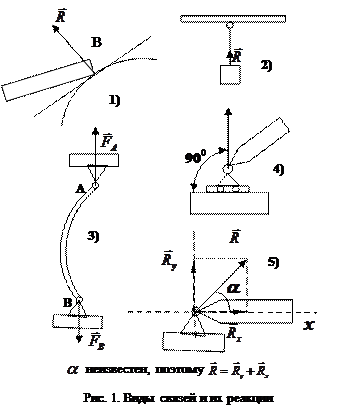
Система сил, линии действия которых лежат в одной плоскости и пересекаются в одной точке, называется плоской системой сходящихся сил. Если силы сходящейся системы приложены к разным точкам тела, то по следствию 1, каждую силу можно перенести в точку О пересечения линий действия и получить эквивалентную систему сил, приложенную в одной точке (рис. 2).

Способы решения задачи сложения сил:

1) графический, с использованием масштаба;

2) вычисления с использованием соответствующих геометрических теорем и тригонометрических зависимостей;

3) методом проекций.

Геометрическое условие равновесия: система сходящихся сил уравновешена тогда и только тогда, когда силовой многоугольник замкнут.

Аналитическое условие равновесия: для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы алгебраические суммы проекций всех сил системы на каждую из двух осей координат были равны нулю.

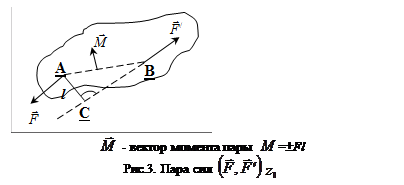
Система двух параллельных сил, равных по модулю и направленных в противоположные стороны называется парой сил. Эта неуравновешенная система производит на тело вращательное действие и не имеет равнодействующей (рис. 3). Вращательный эффект пары измеряется взятым со знаком плюс или минус произведением модуля одной из сил пары на её плечо, это момент пары: 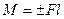(«+» – вращение против часовой стрелки; «–» – вращение по часовой стрелке).

Теорема 1. Пару сил в плоскости её действия можно переносить в любое новое положение, действие пары на тело при этом не изменится.

Теорема 2. Две пары, расположенные в одной плоскости, произведут на тело одинаковое вращательное действие в том случае, если их моменты равны.

Сложение пар сил осуществляется по теореме:

Система пар, действующих на тело в одной плоскости, эквивалентна паре с моментом, равным алгебраической сумме моментов пар систем.

Условие равновесия системы пар:

Для равновесия системы пар сил, действующих на тело в данной плоскости, необходимо и достаточно, чтобы алгебраическая сумма их моментов была равна нулю.

Момент силы относительно точки: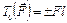

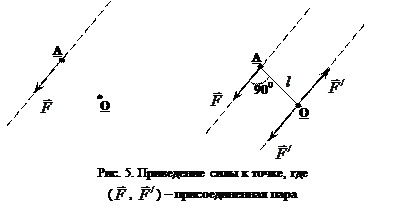
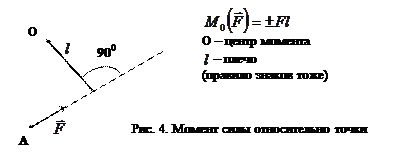В начале прошлого века Л. Пуансо (ввел понятие «пара сил») доказал теорему о переносе силы в любую выбранную точку. Её смысл, всякую силу 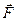, приложенную к телу в точке А, можно переносить параллельно линии её действия в любую точку О, присоединив пару сил, момент которой равен моменту данной силы относительно новой точки её приложения. Это приведение силы к точке (рис.5).

Рассмотрим приведение к точке плоской системы произвольно расположенных сил. Пусть задана система сил: 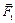, , 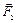, , 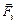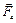они не параллельны друг другу и линии их действия не пересекаются в одной точке. Выберем произвольную точку О – центр приведения и приведём к ней силы, путем переноса в точку О с присоединением пар с моментами 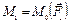, , 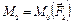, 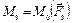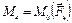. С помощью силового многоугольника, найдём силу эквивалентную системе приведенных сил 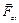(главный вектор системы). Сложив алгебраические моменты присоединенных пар, найдём момент одной эквивалентной им пары: 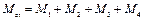(главный момент системы).

Таким образом, произвольная плоская система сил эквивалентна одной силе – главному вектору и одной паре, момент которой равен главному моменту (рис. 6).

Теорема Вариньона: Момент равнодействующей произвольной плоской системы сил относительно любой точки равен алгебраической сумме моментов сил системы, взятых относительно той же точки.

Частные случаи:

1) , 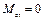– плоская система сил сразу же привилась к равнодействующей.

2) 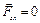, 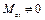– плоская система сил равнодействующей не имеет, она эквивалентна паре сил с моментом .

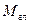3) 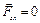и 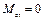– плоская система сил уравновешена. Это и есть условие равновесия.

Задача сложения пространственной (произвольной) системы сил решается аналогично.

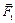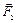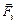Рассмотрим сложение параллельных сил. Представим, что к трём точкам А ₁, А ₂ и А₃ твердого тела приложены параллельные силы , и , образующие пространственную систему. Равнодействующая двух параллельных сил равна по модулю сумме их модулей, а линия действия делит расстояние между точками приложения слагаемых сил на отрезки, обратно пропорциональные силам (рис. 7).

Точка С, через которую проходит линия действия равнодействующей системы параллельных сил, называется центром параллельных сил.

Формулы координат центра параллельных сил имеют вид:

; ; .

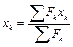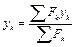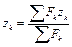Центром тяжести тела называется центр параллельных сил тяжести всех частиц тела. Через центр тяжести проходит линия действия силы 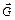– равнодействующей сил тяжести при любом положении тела относительно поверхности Земли. Аналогично записываются формулы координат центра тяжести тела.

При решении задачи нахождения центра тяжести плоской фигуры используется понятие статического момента площади относительно оси. Это алгебраическая сумма произведений площадей частей плоской фигуры на расстояние их центров тяжести до ос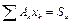и: и 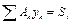. Тогда, если А – площадь всей плоской фигуры,

; .

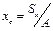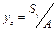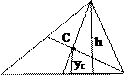
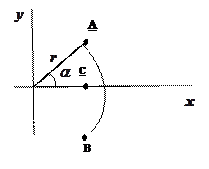
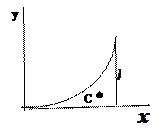
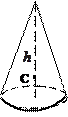
При решении конкретных задач необходимо учитывать симметрию плоских фигур. Центр тяжести – это центр симметрии, он принадлежит оси симметрии.

Примеры:

1) дуга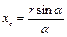

2) треугольник – центр пересечения медиан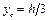

3) круговой сектор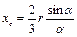

4) параболический треугольник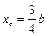

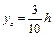
5) конус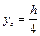

Известны следующие способы нахождения центра тяжести:

1) способ отрицательных площадей;

2) способ подвешивания;

3) способ взвешивания.

4) способ симметрии;

5) способ разбиения на более простые фигуры.

Дата добавления: 2014-12-08