Расчеты на прочность и жесткость стержней при растяжении и сжатии

Теоретический материал лекции №6-7

Продольная сила

При растяжении и сжатии в поперечных сечениях стержня появляется единственное внутреннее усилие N (продольная сила).

Для определения значения N используется метод сечений. Продольную силу считаем положительной если она направлена от сечения, в противном случае – отрицательной. Продольную силу N следует всегда направлять в положительную сторону. На рис. 11 представлен стержень растянутый силой F. От начала координат на расстоянии Z проводим произвольное сечение I-I и отбросим правую сторону (рис. 11). Для определения значения N составляем уравнение статики.

N_1-2 =F

Если рассмотреть равновесие элемента с правой стороны:

N_1-2 =F

Найденные значения N в обеих случаях одинаковы.

Рассмотрим стержень, на который действуют несколько внешних сил на разных участках стержня (рис. 12). Требуется построить эпюру продольной силы. Применяя метод сечений для каждого участка записываем выражения продольной силы

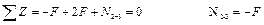
Уравнения показывают закон распределения продольной силы на рассматриваемом участке.

График распределения N по длине стержня называется эпюрой. Для построения эпюры продольной силы N проводим прямую параллельную оси стержня. Перпендикулярно к оси в определенном масштабе откладываем величину N (рис. 12).

На рис. 13 показан прямой стержень длиной l (площадь поперечного сечения А), испытывающий действие силы тяжести (плотность материала g) и сосредоточенной силы F. Требуется найти продольную силу.

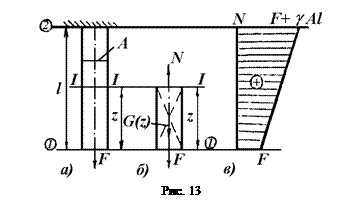
Применяя метод сечений (рис. 13, б), из уравнения равновесия определяем значение продольной силы

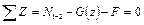
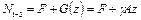
Как видно из рис. 13, в, эпюра продольной силы является линейной функцией от Z. Из уравнения имеем.

Дата добавления: 2014-12-08