Методы решения системы линейных уравнений

1. Правило Крамера. Оно применяется в случае, когда m = n и когда определитель матрицы системы отличен от нуля.

Теорема. Если определитель матрицы системы отличен от нуля, то система совместна и имеет единственное решение:

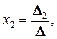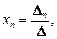…, (8)

где — определитель матрицы системы, а — вспомогательные определители, полученные из заменой j-го столбца столбцом свободных членов.

Пример. Решить систему уравнений

Решение. Находим определитель данной системы:

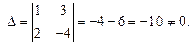Система совместна. Имеем:

Следовательно,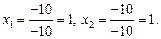

Ответ: .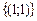

2. Метод обратной матрицы. Он также применяется в случае, когда m = n и 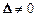. Систему

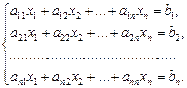(9)

можно записать в матричном виде А · Х = В, где

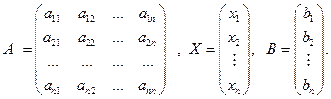
Умножив обе части уравнения слева на А ^–1, получим

X = A ^–1 · B. (10)

Пример. Решить систему уравнений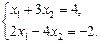

Решение. Из решения рассмотренного ранее примера,

.

Тогда по формуле (10) получим: X = A ^–1 · B = =
= = = .

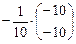Ответ: .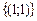

3. Метод Гаусса(метод исключения неизвестных). Он применяется для решения системы (7) в произвольном случае.

Преобразования, аналогичные элементарным преобразованиям над строками расширенной матрицы системы (7), будем называть элементарными преобразованиями этой системы. К ним отнесем еще удаление из системы уравнений типа 0 = 0.

В случае совместности системы (7) она может быть приведена при помощи элементарных преобразований к виду

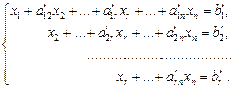(11)

Очевидно, число r равно рангу матрицы системы (который в случае совместности системы совпадает с рангом расширенной матрицы). Это число называется рангом системы. Очевидно, что r n.

Если r = n, тогда система имеет единственное решение.

Пример. Решить систему уравнений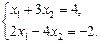

Решение. Из второго уравнения системы вычитаем первое, умноженное на 2. Получаем

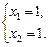
Ответ: .

Если r n, то система (7) в этом случае имеет бесконечное множество решений.

Систему (11) запишем в виде

(12)

Неизвестным x_{r +1},…, x_n присваиваются любые значения, и поэтому они называются свободными. Неизвестные x ₁, x ₂,…, x_r называются базисными. Двигаясь снизу вверх, находим значения всех неизвестных .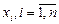

Дата добавления: 2014-12-08