
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вопросы для самопроверки. 1. Что называется n-мерным арифметическим пространством?
|
|
|
|
1. Что называется n -мерным арифметическим пространством?
2. Что называется скалярным произведением двух векторов?
3. Какие системы векторов называются линейно независимыми?
4. Что называется базисом пространства Rn?
5. Что называется матрицей? Как определяются действия над матрицами?
6. Каково правило вычисления определителей второго и третьего порядков?
7. Как вводится понятие определителя в общем случае?
8. Как вводятся минор и алгебраические дополнения к элементу aij?
9. Какая матрица называется обратной по отношению к данной? Всегда ли к данной матрице существует обратная?
10. Каково правило нахождения обратной матрицы?
11. Как найти ранг матрицы?
12. Какая система линейных уравнений называется совместной? Каковы необходимое и достаточное условия совместности системы?
13. Какие существуют методы решения системы линейных уравнений? В чем их суть?
14. В каком случае система линейных уравнений имеет единственное решение, бесконечное множество решений?
Типовая задача 3
Даны векторы 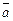 = (2;–1;3),
= (2;–1;3), 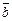 = (1;2;–3),
= (1;2;–3), 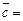 (0;1;2),
(0;1;2), 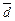 = (–1;9;–13)
= (–1;9;–13)
со своими координатами в базисе  . Показать, что векторы
. Показать, что векторы 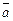 ,
, 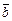 ,
,  сами образуют базис, и найти разложение вектора
сами образуют базис, и найти разложение вектора 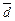 в новом базисе.
в новом базисе.
Решение. Вычисляем определитель, составленный из координат этих векторов: 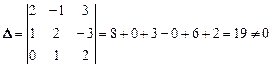 .
.
По теореме 1, сформулированной выше, векторы 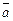 ,
, 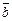 ,
,  образуют базис пространства R 3.
образуют базис пространства R 3.
Пусть 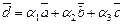 — разложение вектора
— разложение вектора 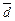 по базису
по базису 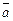 ,
, 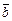 ,
,  .
.
По условию задачи имеем:
–1· 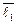 + 9 ·
+ 9 · 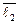 – 13 ·
– 13 · 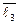 =
= 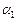 · (2 ·
· (2 · 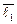 – 1 ·
– 1 · 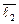 + 3·
+ 3· 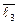 ) +
) +
+ 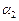 · (1 ·
· (1 · 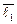 + 2 ·
+ 2 · 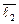 – 3 ·
– 3 · 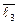 ) +
) + 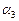 · (0 ·
· (0 · 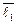 + 1 ·
+ 1 · 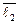 + 2·
+ 2· 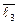 ),
),
–1· 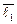 + 9 ·
+ 9 · 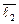 – 13 ·
– 13 · 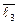 = (2 ·
= (2 · 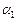 + 1 ·
+ 1 · 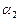 + 0 ·
+ 0 · 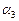 ) ·
) · 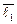 +
+
+ (–1 · 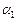 + 2 ·
+ 2 · 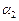 + 1 ·
+ 1 · 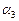 ) ·
) · 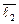 + (3 ·
+ (3 · 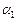 – 3 ·
– 3 · 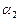 + 2 ·
+ 2 · 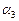 ) ·
) · 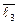 .
.
Из условия равенства двух векторов получим:
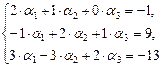
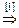
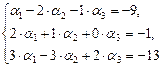
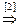
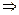
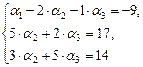
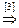
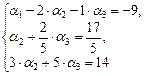
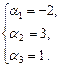
[1]: Обе части второго уравнения умножим на (–1). Поменяем местами первое и второе уравнения.
[2]: Обе части первого уравнения умножим на (–2) и прибавим соответственно ко второму уравнению. Затем обе части первого уравнения умножим на (–3) и прибавим соответственно к третьему уравнению.
[3]: Обе части второго уравнения разделим на 5.
[4]: Обе части второго уравнения умножим на (–3) и прибавим соответственно к третьему уравнению. Из третьего уравнения системы 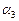 = 1. Подставим это значение во второе уравнение и получим
= 1. Подставим это значение во второе уравнение и получим 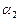 = 3. Подставляя полученные значения
= 3. Подставляя полученные значения 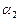 = 3,
= 3, 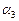 = 1 в первое уравнение, найдем
= 1 в первое уравнение, найдем 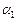 = –2.
= –2.
Итак, 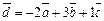 .
.
Ответ: 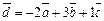 .
.
Типовая задача 4
Исследовать на совместность и решить систему уравнений
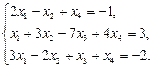
Решение. Находим ранги матрицы системы и расширенной матрицы:
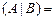

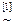
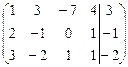
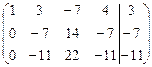

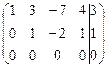 .
.
[1]: Меняем местами первую и вторую строки.
[2]: Элементы первой строки умножим на (–2) и прибавим соответственно к элементам второй строки. Затем элементы первой строки умножим на (–3) и прибавим соответственно к элементам третьей строки.
[3]: Элементы первой строки разделим на (–7), а элементы второй строки — на (–11).
[4]: Из элементов второй строки вычтем элементы третьей строки.
Итак, 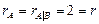 .
.
По теореме Кронекера-Капелли система совместна.
Так как 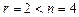 , то система имеет бесконечное множество решений.
, то система имеет бесконечное множество решений.
При помощи элементарных преобразований над уравнениями системы, аналогичных приведенным элементарным преобразованиям над строками матрицы, данная система приводится к виду
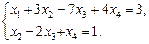
Перенеся члены со свободными неизвестными в правые части системы, получим: 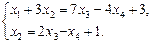
Давая свободным неизвестным х 3, х 4 произвольные значения t 1, t 2, получим общее решение системы: 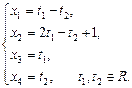
Ответ: 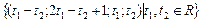 .
.
3. Задание 5
по теме «Теория пределов»
Краткие теоретические сведения
|
|
|
|
|
Дата добавления: 2014-12-08; Просмотров: 394; Нарушение авторских прав?; Мы поможем в написании вашей работы!