Вопросы для самопроверки. 1. Что такое числовая последовательность?

1. Что такое числовая последовательность?

2. Дайте определение предела функции. Может ли функция в точке иметь два предела?

3. Какая функция называется элементарной? Каким замечательным свойством она обладает?

4. Какие вы знаете свойства пределов?

5. Дайте определения бесконечно малой и бесконечно большой функций. Какая между ними существует связь?

6. Сформулируйте первый и второй замечательные пределы.

7. Как вычислить предел вида 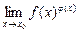? Какие могут встретиться ситуации при его вычислении?

8. Какие две величины называются эквивалентными бесконечно малыми?

9. Перечислите основные эквивалентные бесконечно малые величины.

10. Каким образом применяются эквивалентные бесконечно малые величины при вычислении пределов? Приведите примеры.

Типовая задача 5

Вычислить пределы следующих функций:

1) 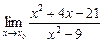при а) х ₀ = 2; б) х ₀ = 3; в) х ₀ = ;

2) ;

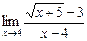3) ;

4) .

Решение. 1а) Функция 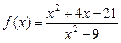является элементарной и определенной в точке х ₀ = 2. По теореме о пределе для элементарной функции,

= = .

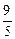1б) Если применить теоремы о пределах сразу, то получим неопределенность типа , поэтому преобразуем числитель и знаменатель функции:

= = = = = .

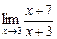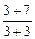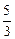1в) Применив теоремы о пределах сразу, получим неопределенность типа . Поэтому для предварительного преобразования выражения функции разделим числитель и знаменатель на старшую степень переменной, т. е. на х ²:

= = =

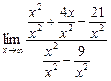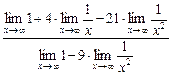= = = 1.

2) Если будем применять теоремы о пределах сразу, то получим неопределенность типа . Для преобразования функции умножим числитель и знаменатель дроби на выражение , сопряженное числителю:

= = =
= = =
= = = .

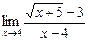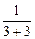3) Применив очевидные преобразования и первый замечательный предел, получим:

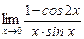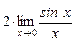= = = = 2 · 1 = 2.

4) При применении теорем о пределах сразу, получаем неопределенность типа [ ]. Применяя второй замечательный предел, получим:

= [ ] = =
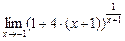= = е ⁴.

Ответ: 1а) 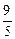; 1б) 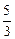; 1в) 1; 2) ; 3) 2; 4) е ⁴.

4. Задания 6 и 7
по теме «Производная и ее применение
для исследования функций»

Дата добавления: 2014-12-08