Вопросы для самопроверки. 1. Дайте определение производной

1. Дайте определение производной. Каков ее геометрический смысл?

2. Какие вы знаете экономические интерпретации производной функции? Приведите примеры.

3. Пусть функция y = f (x) является в некоторой точке дифференцируемой. Следует ли отсюда, что она является непрерывной в этой точке?

4. Сформулируйте общие правила дифференцирования функций и формулы нахождения производных основных элементарных функций.

5. Что называется дифференциалом функции? По какой формуле он вычисляется?

6. Для раскрытия каких неопределенностей может быть использовано правило Лопиталя? Приведите примеры.

7. Как определяются асимптоты кривой? Каким образом они находятся?

8. Какие вы знаете признаки возрастания и убывания функции? Покажите, что функция у = ln x возрастает, а функция у = cos x – 2 x убывает при всех .

9. Что называется экстремумом функции? Сформулируйте достаточное условие его существования.

10. Дайте определение выпуклости, вогнутости графика функции на интервале. Сформулируйте достаточные условия существования этих свойств у графика.

11. Какая точка называется точкой перегиба графика функции? Какое вы знаете достаточное условие существования перегиба в точке?

12. Какова схема исследования функции и построения ее графика?

Типовая задача 6

Найти производные следующих функций:

1) у = (ln² x + 5 x)¹⁰;

2) у = (5 ^{cos 3 x} + x) · tg 3 x;

3) .

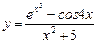Решение. Используя формулы и правила дифференцирования, находим производные данной функции следующим образом:

1) 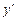= ((ln² x + 5 x)¹⁰) ' = 10 · (ln² x + 5 x)⁹ · (ln² x + 5 x) ' = 10 · (ln² x +
+ 5 x)⁹ · 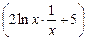= 10 · (ln² x + 5 x)⁹ · .

2) 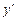=((5 ^{cos 3 x} + x) · tg 3 x) ' = (5 ^{cos 3 x} + x) ' · tg 3 x + (5 ^{cos 3 x} + x) · (tg 3 x) ' =
= (5 ^{cos 3 x} · ln5 · (cos 3 x) ' + 1) · tg 3 x + (5 ^{cos 3 x} + x) · · 3 = (–5 ^{cos 3 x} · ln5 · · sin 3 x · 3 + 1) · tg 3 x + (5 ^{cos 3 x} + x) · = (–3 · ln5 · 5 ^{cos 3 x} · sin 3 x +
+ 1) · tg 3 x + .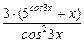

3) = =

= =

= .

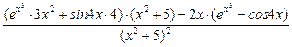Ответ: 1) 10 · (ln² x + 5 x)⁹ · ;

2) (–3 · ln5 · 5 ^{cos 3 x} · sin 3 x + 1) · tg 3 x + ;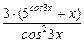

3) .

Типовая задача 7

Исследовать функцию у = и построить ее график.

Решение. 1. Так как функция не определена при х + 1 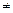0 (х 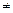–1), то D (y) = .

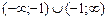2. Функция является ни четной, ни нечетной, так как D (y) не является симметричной относительно начала координат.

3. Функция является непериодической.

4. Находим асимптоты.

х = –1 — точка разрыва. Если х будет стремиться к (–1) слева, оставаясь меньше (–1), то (х + 1)² — положительная бесконечно малая функция, а — положительная бесконечно большая функция, т. е. если , то (х + 1)² +0, а , или .

Аналогично показывается, что .

Делаем вывод, что прямая х = –1 — вертикальная асимптота
графика.

Для нахождения наклонных асимптот у = k · x + b при
находим пределы:

k = = = =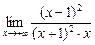
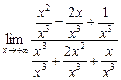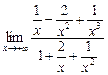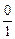= = = = 0,

b = = = =
= = = 1.

Таким образом, у = 1 — горизонтальная асимптота графика.

Аналогичным образом показывается, что у = 1 — горизонтальная асимптота и при х .

5. = =
= = = .

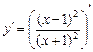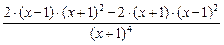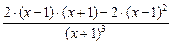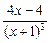6. Находим критические точки. Решаем уравнение y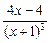' = 0:

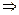
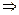
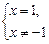
= 0 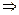x = 1.

Точка х = –1, в которой производная не существует, не принадлежит D (y). Точка х = 1 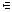D (y). Поэтому х = 1 — единственная критическая точка.

7. Критическая точка х = 1 разбивает область определения на интервалы. Определим знак первой производной у' на каждом интервале (рис. 14).

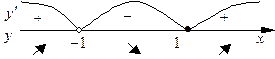
Рис. 14

.

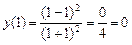Составим следующую таблицу:

х	(– 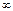; –1)	–1	(–1; 1)		(1; )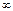
y'	+	Не существует	–		+
у	Возрастает	Не существует	Убывает		Возрастает
		Экстремума нет		min

8. = =
= = =
= = .

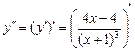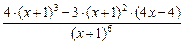9. Решим уравнение 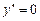: = 0.

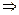
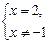
Отсюда 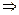х = 2.

Точка х = –1, в которой вторая производная не существует, не принадлежит D (y). Точка х = 2 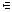D (y). Определим знак второй производной на области определения (рис. 15).

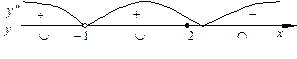
Рис. 15

.

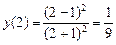Составим следующую таблицу:

х	(– 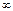; –1)	–1	(–1; 2)		(2; )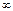
y''	+	Не существует	+		–
у		Не существует		1/9
	График вогнутый	Перегиба нет	График вогнутый	Точка перегиба	График выпуклый

10. Находим точки пересечения графика с осями координат.

10.1. С осью Ох. Так как у = 0, то имеем

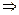
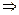
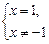
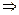х = 1.

10.2. С осью Оу. Так как х = 0, то имеем у = .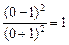

Значит, (1,0), (0,1) — точки пересечения с осями координат.

Так как числитель и знаменатель дроби являются полными квадратами, то 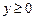при всех х 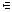D (y).

11. По результатам исследования строим график функции (рис. 16).

Рис. 16

Дата добавления: 2014-12-08