Контрольная работа № 3

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К КОНТРОЛЬНЫМ РАБОТАМ

Тема 5. Теория вероятности.

Основные понятия теории вероятности. Относительная частота.

Определения совместимых и несовместимых событий. Теоремы сложения вероятности и следствия из неё. Определения зависимых и независимых событий. Теоремы умножения вероятности. Условная вероятность. Формула полной вероятности. Формула Байеса. Повторные независимые испытания.Формула Бернулли. Теорема Пуассона. Локальная теорема Муавра-Лапласа. Интегральная теорема Лапласа. Закон распределения дискретной случайной величины. Математическое ожидание дискретной случайной величины и его свойства. Дисперсия дискретной случайной величины и её свойства.

Вопросы для самоконтроля.

1. Основные понятия теории вероятности.

2. Определения совместимых и несовместимых событий. Теоремы сложения вероятности и следствия из неё.

3. Определения зависимых и независимых событий. Теоремы умножения вероятности.

4. Условная вероятность

5. Формула полной вероятности.Формула Байеса.

6. Повторные независимые испытания.Формула Бернулли.

7. Теорема Пуассона. Локальная теорема Муавра-Лапласа. Интегральная теорема Лапласа.

8. Закон распределения дискретной случайной величины. Математическое ожидание и дисперсия дискретной случайной величины и их свойства.

Основные правила интегрирования.

1. Интеграл от суммы конечного числа функций равен сумме интегралов от слагаемых функций.

2. Постоянный множитель подынтегральной функции можно вынести за символ интеграла.

Пример 1.

Найти . Решение:

.

Ответ: .

3. Всякая формула интегрирования сохраняет свой вид при подстановке вместо независимой переменной любой дифференциальной функции от неё, т.е. если 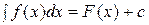, то и , где .

Это правило очень важно. Основная таблица интегралов в силу этого правила оказывается справедливой независимо от того, является ли переменная интегрирования независимой или любой дифференцируемой функцией её.

Преобразование , где , называется подведением под знак дифференциала.

Очень часто применяются следующие преобразования дифференциалов:

1) ;

2) ;

Примеры.

1) .

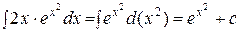2) .

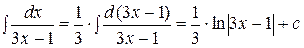3) .

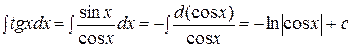Методы интегрирования.

1. Метод подстановки.

Полагая, что 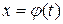, где – новая переменная, – непрерывно дифференцируемая функция. Будем иметь:

.

Функцию стараются выбирать т.о., чтобы правая часть формулы приобрела более удобный для интегрирования вид.

Пример 1.

Найти 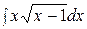. Решение:

Замену сделаем т.о., чтобы избавиться от корня: 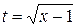. Отсюда выразим: .

.

Ответ: .

2. Интегрирование по частям.

Если и – непрерывно дифференцируемые функции, то имеет место формула интегрирования по частям:

.

1) Интегралы вида , , 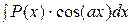, 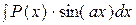где – многочлен степени .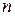

В этих интегралах за 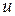принимают многочлен, а всё остальное в подынтегральном выражении – за .

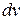Пример 1.

Найти . Решение:

.

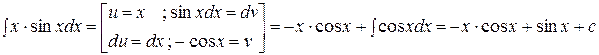Ответ: .

2) Интегралы вида , , , , , 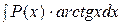где – многочлен степени .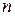

В этих интегралах за 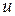принимают логарифмическую функцию или -функцию, а остальное – за .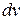

Пример 1.

Найти . Решение:

.

Ответ: .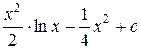

3) Интегралы вида , .

При вычислении этих интегралов формула интегрирования по частям применяется дважды. Оба раза за 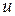принимается либо показательная, либо тригонометрическая функция.

Пример 1.

Найти 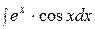. Решение:

;

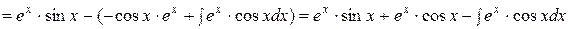Обозначим 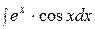за 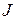. Тогда:

;

;

.

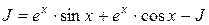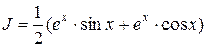Ответ: .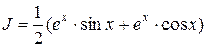

Свойства определённого интеграла.

1. Интеграл от суммы конечного числа функций равен сумме интегралов от слагаемых функций.

2. Постоянный множитель подынтегральной функции можно вынести за символ интеграла.

.

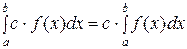3. Если верхний и нижний пределы интеграла поменять местами, то интеграл изменит только знак.

.

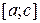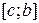4. Если предел интегрирования разбит на две части и , то

.

Формула Ньютона-Лейбница.

Значение определённого интеграла равно разности значений любой первообразной от подынтегральной функции, взятых при верхнем и нижнем пределах интеграла.

.

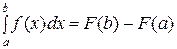Несобственные интегралы.

Несобственным интегралом от функции f(x) в интервале 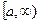называется предел интеграла

при . Записывается это так:

Если указанный предел существует, то несобственный интеграл называется сходящимся, а если не существует, то расходящимся.

Если первообразная функция F(x) для подынтегральной функции f(x) известна, то легко установить, сходится несобственный интеграл или нет. С помощью формулы Ньютона-Лейбница получаем

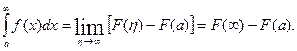
Таким образом, если предел первообразной F(x) при существует(он обозначен через 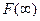), то несобственный интеграл сходится, а если этот предел не существует, то интеграл расходится.

Примеры.

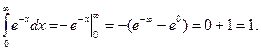№1.

Следовательно, несобственный интеграл сходится и равен 1.

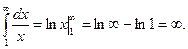
№2.

Интеграл расходится, так как первообразная lnx при стремится к бесконечности.

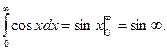
№3.

Интеграл расходится, так как величина не стремится к пределу при (колеблется).

Аналогично определяется несобственный интеграл в интервале

,

где предел первообразной F(x) при

Если функция f(x) определена и непрерывна на всей числовой оси, то можно рассматривать и несобственный интеграл в интервале 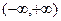. По определению

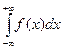
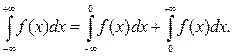
Если оба интеграла в правой части сходятся, интеграл называется сходящимся.

Если первообразная F(x) известна, то , где под символами понимают пределы к которым стремится F(x) соответственно при Если хотя бы один из этих пределов не существует, то несобственный интеграл расходится.

№4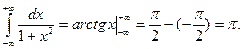

Приложение определенного интеграла

Дата добавления: 2014-12-27