
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Дифференциальные уравнения второго порядка
|
|
|
|
Дифференциальными уравнениями второго порядка называют уравнения вида 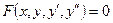 , в левую часть которых входит вторая производная неизвестной функции.
, в левую часть которых входит вторая производная неизвестной функции.
Частные случаи уравнений второго порядка.
- Правая часть уравнений не содержит
 и
и 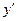 :
: 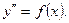
Так как 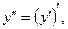 то
то 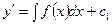 интегрируя ещё раз, будем иметь
интегрируя ещё раз, будем иметь  где
где 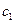 и
и 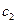 - произв. постоянные.
- произв. постоянные.
- Правая часть уравнения не содержит
 :
:
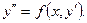
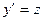 , тогда
, тогда 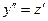 и преобразуем уравнение к виду:
и преобразуем уравнение к виду: 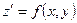 .
.
Если найдём решение уравнения  то искомое решение получим интегрированием равенства
то искомое решение получим интегрированием равенства 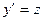 .
.
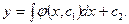
Пример
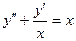
Полагая 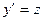 и
и 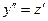 , получим:
, получим:  , которое является линейным.
, которое является линейным.
Решим сначала однородное уравнение:
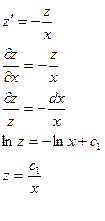
Пусть 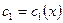
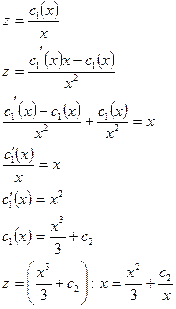
Тогда 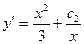
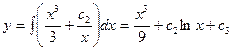
3. Правая часть уравнения не содержит x: 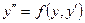
Положим 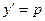 и будем считать p функцией от y. Дифференцируя это равенство, получим
и будем считать p функцией от y. Дифференцируя это равенство, получим  . Чтобы исключить x, произведём следующее преобразование:
. Чтобы исключить x, произведём следующее преобразование: 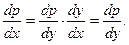
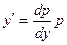 .
.
Т.о. 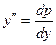 Подставив в уравнение, будем иметь
Подставив в уравнение, будем иметь 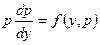 , т.е. уравнение первого порядка относительно p как функции от y.
, т.е. уравнение первого порядка относительно p как функции от y.
Пример: 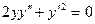
Полагая 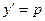 и
и 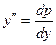 получим,
получим,  .
.
Это уравнение первого порядка с разветвляющимися переменными.
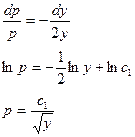
Определим  из уравнения
из уравнения 
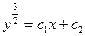
Линейные, неоднородные дифференциальные уравнения II порядка
с постоянными коэффициентами
y′′+py′+qy=f(x) (1)
p,q - действительные числаf(x)-непрерывная функция
Общее решение является суммой частного решения неоднородного уравнения и общего решения однородного уравнения
Если в правой части многочлен, показательная функция, sinbx, cosbx или их линейная комбинация, то частное решение может быть найдено методом неопределенных коэффициентов.
- Правая часть имеет вид:
f(x)=Pn(x),
где
Pn(x)=a0 xn+a1 xn-1+…+an-1 x+an многочлен степени n.
Тогда частное решение можно искать в виде
y*=Qn(x)xr ,
где Qn(x) – многочлен той же степени, что и Pn(x), а r- число корней характеристического уравнения, равных нулю.
Например: y′′-2y′+y=x+1
k2-2k+1=0
(k-1)2=0
k1=k2=1
Общее решение однородного уравнения
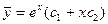
т.к. r =0 (корни характеристического уравнения не равны нулю), то частное решение ищем в виде
y*=(Ax+B)x0=Ax+B
y*=Ax+B
Дважды продифференцируем и подставим в исходное уравнение
(y*)′ =A
(y*)′′=0
0-2A+Ax+B=x+1
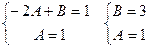
Частное решение данного уравнения имеет вид: y*=x+3
А его общее решение
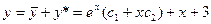
2. Правая часть имеет вид
f(x)=ea xPn(x),
где Pn(x) – многочлен степени n.
Частное решение y* ищут в виде
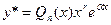 ,
,
где Qn(x)- многочлен той же степени, что и Pn(x)
r – число корней характеристического уравнения равных a. (если a=0, то f(x)=Pn(x) т.е. будет 1 случай).
Например: Найти общее решение уравнения
y′′-4y′+3y=xex
a=1, Pn(x)=x, n=1
k2- 4k+3=0
k1=1, k2=3
Общее решение однородного уравнения
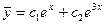
т. к. только один корень k1=a=1, то r=1
Pn(x)=x
Частное решение ищем в виде:
y*=(Ax+B)xex=(Ax2+Bx)ex
(y*)′=(Ax2+Bx)ex+ (2Ax+B)ex=
=ex(Ax2+Bx+2Ax+B)
(y*)′′= ex(Ax2+Bx+2Ax+B)+ ex(2Ax +B +2A)
Подставим в исходное уравнение:
ex(Ax2+Bx+4Ax+2B+2A-4Ax2-4Bx-8Ax-
-4B+3Ax2+3Bx)=xex: ex
x(-4A)+2A-2B=x
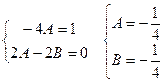
Общее решение уравнения:
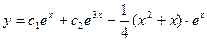
3. Правая часть имеет вид:
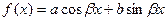 ,
,
где a,b,b – известные числа. Тогда частное решение ищут в виде:
y*=(Acos b x+Bsinb x) xr,
где A и B неизвестные коэффициенты,
r -число корней характеристического уравнения, равных ib.
Например: y ′′ + y = sinx
a=0, b=1, b=1
k2+1=0
k1=i, k2=-i
Общее решением однородного уравнения:

так как bi=i корень характеристического уравнения, то r = 1.
Частное решение ищем в виде: y*=(Acosx+Bsinx)x
(y*)′=(Acosx+Bsinx)x+x(-Asinx+Bcosx)
(y*)′′=-Asinx+Bcosx+Bcosx-Asinx+
+x(-Acosx-Bsinx)
- Asinx+Bcosx+Bcosx-Asinx-xA cosx -
-xB sinx+xA cosx+Bsinx=sinx
-2Asinx+2Bcosx=sinx
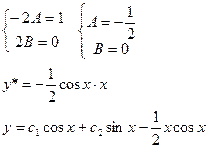
IY. Правая часть имеет вид
f(x)=eax(Pn(x)cosb x+Pm(x)sinb x),
где Pn(x) - многочлен степени n,
Pm(x) - многочлен степени m.
Тогда частное решение ищут в виде:
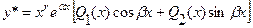
где Q1 и Q2 многочлены степени S, S=max(n;m,)r - число корней характеристического уравнения, равных a+b i.
Например: y′′-y=3e2xcosx/
a =2 b=1
k2 -1=0
k 1=1 k 2=-1
Общее решение однородного уравнения
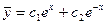
В правой части Pn=3 n=0,
Pm=0 m=0, Þ S=0
a + b i=2+ i -не являeтся корнем характеристического уравнения, следовательно частное решение ищем в виде: y*=e2x(Acosx+Bsinx)
(y*)′ =2e2x(Acosx+Bsinx)+
+ e2x(-A sinx+Bcosx)=
= e2x(2Acosx+2Bsinx –Asinx+Bcosx)
(y*)′′= 2 e2x(2Acosx+2Bsinx –Asinx+Bcosx)+
+ e2x(-2Asinx+2Bcosx –Acosx-Bsinx)
подставим y*, (y*)′′ в уравнение:
4Acosx+4Bsinx-2Asinx+2Bcosx-2Asinx+2Bcosx-Acosx-Bsinx+
+Acosx+Bsinx=3cosx
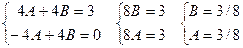

Общее решение 
Теорема: Если 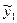 – решение уравнения
– решение уравнения
y′′+py′+qy=f1(x),
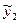 - решение уравнения
- решение уравнения
y′′+py′+qy=f2(x),
то сумма 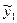 +
+ 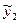 является решением
является решением
y′′+py′+qy=f1(x)+ f2(x)
Например: y′′-2y′+ y= sinx+e - x
k2-2k+1=0
k1=k2=1,
тогда общее решение однородного уравнения будет в виде

Частное решение уравнения будет в виде
y*=y1*+y2*
где y1* –решение уравнения
y′′-2y′+ y= sinx
Где y2*- решение уравнения
y′′-2y′+ y= e-x
1. Найдем частное решение y1*, т.к. ib=i не является корнем характеристического уравнения (r=0), то решение
y1*=Asinx+Bcosx
(y1*)′= Acosx-Bsinx
(y1*)′′=-Asinx-Bcosx
Подставим в уравнение
-Asinx-Bcosx--2Acosx +2Bsinx+ Asinx+ Bcosx =sinx

y1*=1/2 cosx
2. Найдем частное решение y2*
y2*=Ae-x
т.к. a =-1 не является корнем характеристического уравнения.
(y2*)′= -Ae - x
(y2*)′′=Ae - x
Ae – x -2(-Ae - x)+Ae –x = e - x
4A=1 Þ A=1/4
y2*=1/4 e-x
Таким образом, частное решение данного уравнения y*=y1*+y2*=1/2 cosx+1/4e-x
Общее решение уравнения
y = 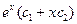 + 1/2 cosx+1/4e-x
+ 1/2 cosx+1/4e-x
Неоднородные уравнения
высших порядков
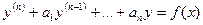 , (1)
, (1)
где 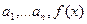 -непрерывные функции от x (или постоянные числа)
-непрерывные функции от x (или постоянные числа)
 (2)
(2)
Теорема: Если 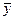 – общее решение однородного уравнения (2), а y *– частное решение неоднородного уравнения (1), то
– общее решение однородного уравнения (2), а y *– частное решение неоднородного уравнения (1), то
Y = 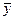 + y *
+ y *
- общее решение неоднородного уравнения (1).
Например: yIY- y =x3+ 1
k4-1=0
k1= 1, k2=- 1 ,k3=i, k4= -i.
Общее решение однородного уравнения
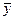 = c1ex+c2 e -x+c3 cosx+c4 sinx
= c1ex+c2 e -x+c3 cosx+c4 sinx
Частное решение неоднородного уравнения ищем в виде
y*=A0x3+A1 x 2+A2 x +A3
(y*)′=3A0 x 2+2A1 x +A2
(y*)′′=6A0 x +2A1
(y*)′′′=6A 0
yIY=0
0 - A0 x 3-A1 x 2-A2 x -A3= x 3+ 1
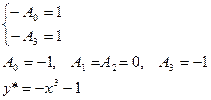
y= c1ex+c2 e -x+c3 cosx+c4 sinx-x3- 1
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 817; Нарушение авторских прав?; Мы поможем в написании вашей работы!