
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Дифференциальные уравнения
|
|
|
|
Контрольная работа №4.
Интегральное исчисление функции одной переменной.
Контрольная работа № 3
1. Вычислить неопределенный интеграл. Правильность вычисления проверить дифференцированием.
1.1. а) 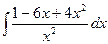 ; б)
; б) 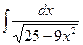 ; в)
; в) 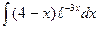 ; г)
; г) 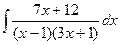
д) 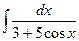 .
.
1.2. а) 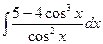 ; б)
; б) 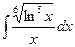 ; в)
; в) 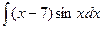 ; г)
; г) 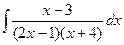 ;
;
д) 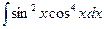 .
.
1.3. а) 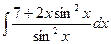 ; б)
; б) 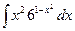 ; в)
; в) 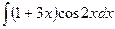 ; г)
; г) 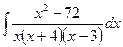 ;
;
д) 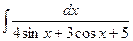 .
.
1.4. а) 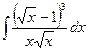 ; б)
; б) 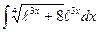 ; в)
; в) 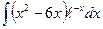 ; г)
; г) 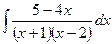 ;
;
д) 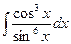 .
.
1.5. а) 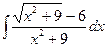 ; б)
; б) 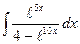 ; в)
; в) 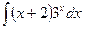 ; г)
; г)  ;
;
д) 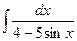 .
.
1.6. а)  ; б)
; б)  ; в)
; в) 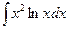 ; г)
; г) 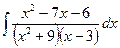 ;
;
д) 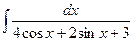 .
.
1.7. а) 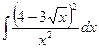 ; б)
; б) 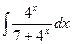 ; в)
; в) 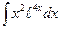 ; г)
; г) 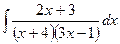 ;
;
д) 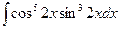 .
.
1.8. а) 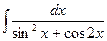 ; б)
; б) 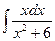 ; в)
; в) 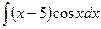 ; г)
; г) 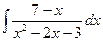 ;
;
д) 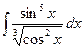 .
.
1.9. а) 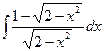 ; б)
; б) 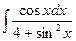 ; в)
; в) 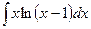 ; г)
; г) 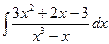 ;
;
д)  .
.
1.10. а) 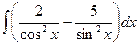 ; б)
; б) 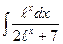 ; в)
; в) 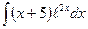 ; г)
; г) 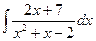 ;
;
д) 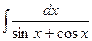 .
.
2. Вычислить определенный интеграл.
2.1. а) 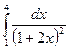 ; б)
; б) 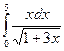 ; в)
; в)  ;
;
2.2. а) 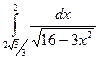 ; б)
; б) 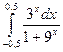 ; в)
; в) 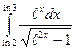 ;
;
2.3. а)  ; б)
; б) 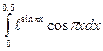 ; в);
; в); 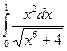
2.4. а) 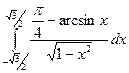 ; б)
; б) 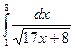 ; в)
; в) 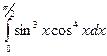 ;
;
2.5. а) 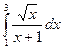 ;б)
;б) 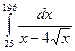 ; в)
; в) 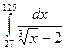 ;
;
2.6. а)  ; б)
; б) 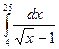 ; в)
; в) 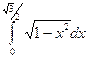 ;
;
2.7. а) 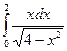 ; б)
; б) 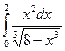 ; в)
; в) 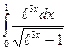 ;
;
2.8. а) 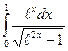 ;б)
;б) 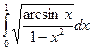 ; в)
; в) 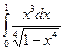 ;
;
2.9. а) 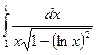 ; б)
; б) 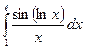 ;в)
;в) 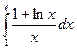 ;
;
2.10.а) 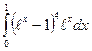 ; б)
; б) 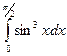 ; в)
; в) 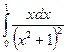 ;
;
3. Вычислить интегралы или установить их расходимость.
3.1. 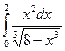 ;
;
3.2. 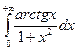 ;
;
3.3. 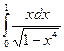 ;
;
3.4. 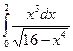 ;
;
3.5. 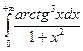 ;
;
3.6. 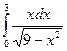 ;
;
3.7. 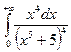 ;
;
3.8. 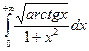 ;
;
3.9. 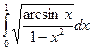 ;
;
3.10. 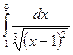 ;
;
4. Вычислить площадь фигуры, ограниченной данными линиями. Сделать чертеж.
4.1. 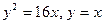 .
.
4.2. 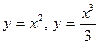 .
.
4.3. 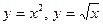 .
.
4.4. 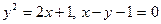 .
.
4.5. 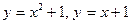 .
.
4.6. 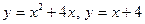 .
.
4.7. 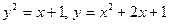 .
.
4.8. 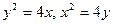 .
.
4.9. 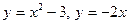 .
.
4.10. 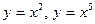 .
.
5. Найти общее решение (общий интеграл) дифференциального уравнения.
5.1. 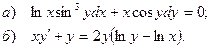
5.2. 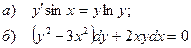
5.3. 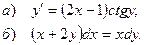
5.4. 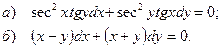
5.5. 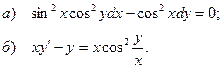
5.6. 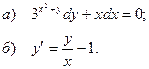
5.7. 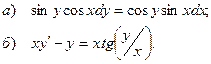
5.8. 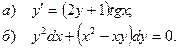
5.9. 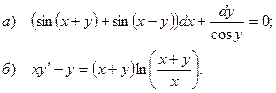
5.10. 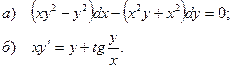
6. Найти частное решение данного дифференциального уравнения, удовлетворяющее данным начальным условиям.
6.1. 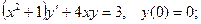
6.2. 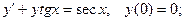
6.3. 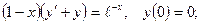
6.4. 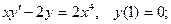
6.5. 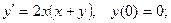
6.6. 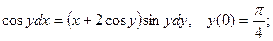
6.7. 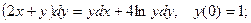
6.8. 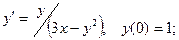
6.9. 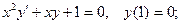
6.10. 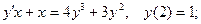
7. Найти общее решение линейного однородного дифференциального уравнения второго порядка.
7.1. 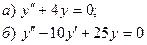 7.6.
7.6. 
7.2. 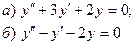 7.7.
7.7. 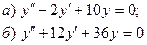
7.3. 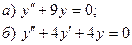 7.8.
7.8. 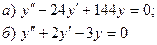
7.4. 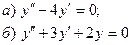 7.9.
7.9. 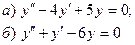
7.5. 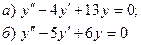 7.10.
7.10. 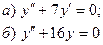
8. Найти частное решение линейного неоднородного дифференциального уравнения, удовлетворяющее данным начальным условиям.
8.1. 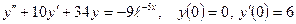
8.2. 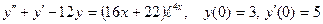
8.3. 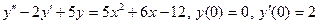
8.4. 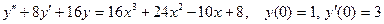
8.5. 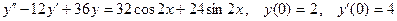
8.6. 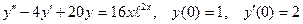
8.7. 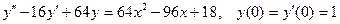
8.8. 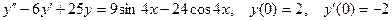
8.9. 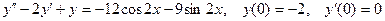
8.10. 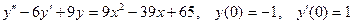
9. Исследовать ряд на сходимость.
9.1. 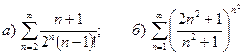
9.2. 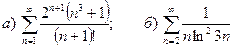
9.3. 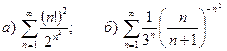
9.4. 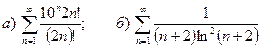
9.5. 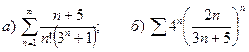
9.6. 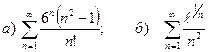
9.7. 
9.8. 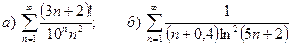
9.9. 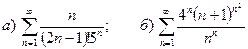
9.10. 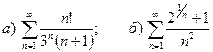
10. Найти область сходимости ряда.
10.1. 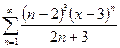 ; 10.6.
; 10.6. 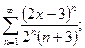
10.2. 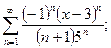 10.7.
10.7. 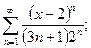
10.3. 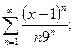 10.8.
10.8. 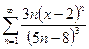 ;
;
10.4. 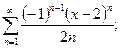 10.9.
10.9. 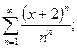
10.5. 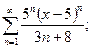 10.10.
10.10. 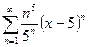 .
.
11. Решить задачи по теории вероятности.
11.1 а) Наборщик пользуется двумя кассами (в одинаковой степени каждой). В первой кассе 90%, а во второй 80% отличного шрифта. Найти вероятность того, что наудачу извлеченная литера из наудачу взятой кассы будет отличного качества.
б)Монету бросают 5 раз. Найти вероятность того, что «герб» выпадет менее 2 раз.
11.2 а) На распределительной базе находятся электрические лампочки, изготовленные на двух заводах. Среди них 60% изготовлено первым заводом и 40% - вторым. Известно, что из которых 100 лампочек, изготовленных первым заводом, 95 удовлетворяют стандарту, а из 100 лампочек, изготовленных вторым заводом, удовлетворяют стандарту 85. Определить вероятность того, что взятая наудачу лампочка будет удовлетворять стандарту.
б) Студентка Петрова не очень добросовестно подготовилась к экзамену. Поэтому вероятность ответить на заданный ей вопрос равна 0,5. Какова вероятность того, что она ответит на три из семи заданных вопросов.
11.3 а)Партия электрических лампочек на 20% изготовлена первым заводом, на 30% - вторым, на 50% - третьим. Вероятности выпуска бракованных лампочек соответственно равны q1 =0,01, q2 =0,005, q3 =0,006. Найти вероятность того, что наудачу взятая из партии лампочка окажется стандартной.
б) Игральный кубик подбрасывается шесть раз подряд. Какова вероятность того, что шестерка выпадет ровно два раза?
11.4 а). На предприятии изготовляются изделия определенного вида на трех поточных линиях. На первой линии производится 30% изделий от общего объема их производства, на второй – 25%, на третьей – остальная часть продукции. Каждая из линий характеризуется соответственно следующими процентами годности изделий: 97%, 98%, 96%. Определить вероятность того, что наугад взятое изделие, выпущенное предприятием, окажется бракованным.
б) Вероятность того, что пассажир опоздает на транзитный автобус, равна 0,01. Найти вероятность того, что на этот рейс опоздают трое из пяти не пунктуальных пассажиров.
11.5 а)В данный район изделия поставляются двумя фирмами в соотношении 2:3. Среди продукции первой фирмы стандартные изделия составляют 90%, второй – 85%. Найти вероятность того, что приобретённое изделие окажется нестандартным.
б) Вероятность того, что вакцина предотвратит у пациента заболевание гриппом, равна 0,9. Найти вероятность того, что три пациента из пяти прошедших вакцинацию, не заболеют гриппом.
11.6 а) В обувной магазин поступает продукция двух фабрик по пошиву обуви: 40% - с первого и 60% - со второго. Среди обуви, поступившей с первой фабрики 2% бракованной, а со второй – 4%. Тогда вероятность того, купленная в этом магазине пара обуви окажется бракованной, равна…
б) Пусть вероятность того, что покупателю необходима обувь 41-го размера, равна 0,2. Найти вероятность того, что из 6 покупателей двум потребуется обувь этого размера.
11.7 а) В данный район изделия поставляются двумя фирмами в соотношении 2:3. Среди продукции первой фирмы стандартные изделия составляют 90%, второй – 85%. Найти вероятность того, что приобретённое изделие окажется нестандартным.
б) Вероятность того, что вакцина предотвратит у пациента заболевание гриппом, равна 0,9. Найти вероятность того, что три пациента из пяти прошедших вакцинацию, не заболеют гриппом.
11.8 а) В центре города находятся два магазина, торгующих бытовой техникой. Вероятность того, что покупатель зайдет за покупкой в любой из них, одинакова. Вероятность того, что в магазине №1 покупатель сможет без очереди приобрести необходимую ему технику, равна 0,3; в магазине №2 – 0,6. Найти вероятность того, что покупатель приобретет без очереди бытовую технику в первом же посещенном им магазине.
б)Монету подбрасывают 8 раз. Какова вероятность того, что она 4 раза упадет гербом вверх?
11.9 а). Два предприятия города хотели бы взять на временную работу студента. Вероятность того, что условия трудового договора устроят студента на первом предприятии, равна 0,8; на втором – 0,3. Студент с равной вероятностью может пойти на любое из данных предприятий, причем в течение одного рабочего дня он может посетить только одно из предприятий. Найти вероятность того, что в первый же день студент устроится на работу на одно из этих предприятий.
б) Монета брошена 5 раз. Какова вероятность того, что «герб» выпадет ровно два раза?
11.10 а) Мастер и его ученик штампуют детали, причем производительность труда мастера в два раза больше производительности труда его ученика. При этом вероятность того, что деталь, изготовленная мастером, будет бракованной, равна 0,05, а учеником – 0,2. Найти вероятность того, что наудачу выбранная деталь окажется бракованной.
б) Вероятность того, что в течение гарантийного срока холодильник данной фирмы выйдет из строя, равна 0,05. Найти вероятность того, что в течении гарантийного срока выйдут из строя три холодильника, приобретенных для школы-интерната.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 2069; Нарушение авторских прав?; Мы поможем в написании вашей работы!