Лабораторная работа 2

Тема: Многофакторное прогнозирование

Цели работы:

1. Выработка практических навыков расчета и оценки адекватности уравнения многофакторной регрессии.

2. Запуск, отладка и тестирование программы расчета коэффициентов и оценки адекватности уравнения многофакторной регрессии.

3. Расчет параметров адекватной многофакторной модели и прогнозирование объема перевозок АК с помощь программы [4,c.76].

Словесная постановка задачи

Имеются исходные данные о величинах х₁, х₂, х₃,... х_p за n лет, влияющих на объем авиаперевозок . Модель имеет вид

y = F (х₁, х₂,... х_i,... х_p) = a₀ + a₁х₁+... + a_i х_i +...+ a_p х_p, (2.1) где a₀, a₁, a₂,... a_i,... a_p - расчетные коэффициенты уравнения.

Задание нa лабораторную работу

В лабораторной работе необходимо:

1. Ввести программу в ЭВМ и создать файл исходных данных.

2. Вычислить модель вида (2.1), используя программу mn_reg.pas.

3. Оценить адекватность модели вида (2.1) и силу факторов х₁ и х₂ .

4. Сформировать прогноз объема перевозок АК.

Методические рекомендации

В классическом регрессионном анализе для расчета коэффициентов уравнения регрессии вида (1.1) используется метод наименьших квадратов (МНК), в основу которого положен алгоритм, минимизирующий

, (2.2)

где n - количество наблюдений исходных данных.

Уравнение для определения вектора расчетных коэффициентов уравнения регрессии y = F (х₁, х₂,... х_i,... х_p) имеет вид

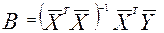, (2.3)

где - матрица исходных значений факторов;

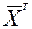- транспонированная матрица ;

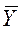- вектор исходных значений моделируемого показателя у.

Алгоритм МНК, решающий уравнение (1.2), имеет вид:

Шаг 1. Транспонируется матрица исходных данных

. (2.4)

Шаг 2. Умножается транспонированная матрица 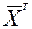справа на матрицу 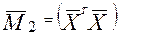. (2.5)

Шаг 3. Обращается матрица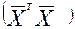

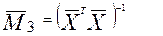. (2.6)

Шаг 4. Умножается справа матрица М3 на матрицу М1

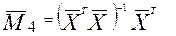. (2.7)

Шаг 5. Умножается справа матрица М4 на вектор У

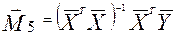. (2.8)

ЭВМ-программа вычислят коэффициенты регрессии a₀,a₁ и a₂ и критерии оценки адекватности уравнения. Адекватность - понятие многоаспектное, оцениваемое совокупностью качественных и количественных критериев. Так, (2.1) адекватно, если знаки при коэффициентах a_i совпадают с физическим смыслом 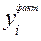. При многофакторном регрессионном моделировании рассматриваются варианты моделей (2.1) и отбирается адекватный вариант модели, который лучшим образом отображает особенности изменения .

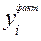Модель (2.1) можно считать адекватной, если имеется полное соответствие структур фактических 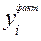и расчетных значений 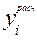, вычисленных по модели (2.1). Для оценки совпадения 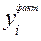и 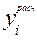используется несколько критериев оценки статистической адекватности и достоверности многофакторной модели, в число которых входят:

1. Критерий Фишера, оценивающий однородность дисперсий

, где (2.9)

- дисперсия показателя у; (2.10)

- математическое ожидание у; (2.11)

- остаточная дисперсия;

p - количество расчетных коэффициентов в модели;

n - объем выборки;

- табличное значение квантили критерия Фишера при доверительной вероятности p_d =90% и входах в табл.3 [1] k1=n-1; k2=n-p-1.

Уравнение регрессии считается адекватным при

max и ≥ (2.12)

2. Коэффициент множественной корреляции R

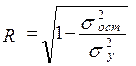, (2.13)

оценивающий гипотезу о линейности формы связи между У и Х. Гипотеза не отвергается при R >= 0.8.

Значимость коэффициента R оценивается с помощью статистики

, (2.14)

где n - объем выборки;

p - число параметров в модели;

- ошибка коэффициента R.

Коэффициент R считается значимым при

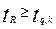, (2.15)

где k = n -1 - число степеней свободы;

q - уровень значимости (рекомендуется выбирать 97.5 - 95%).

3. Коэффициент множественной детерминации

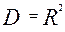(2.16)

Так, если D =0.87, то факторы, включенные в модель, отображают 87% дисперсии У, а 13% приходятся на долю факторов, не включенных в модель.

4. Средняя ошибка аппроксимации

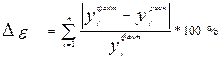(2.17)

Адекватной считается модель, у которого 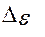<= 2 %.

5. Статистические оценки значимости коэффициентов a_i

(2.18)

где 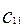- диагональный элемент матрицы ;

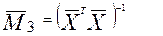- табличное значение критерия Стьюдента (q=0.95,k=n-1).

При незначимости a_i из Х надо удалить х_i с min t_ai и повторить расчет a_i .

6. Критерий Дарбина-Уотсона, указывающий на наличие автокорреляции, если D ≤ 2. 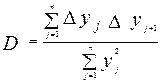(2.19)

где = .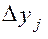

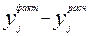7. Матрица коэффициентов парной корреляции R = ,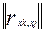

где 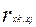- коэффициент парной корреляции между факторами x_k и x_j

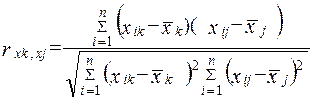. (2.20)

Если хотя бы для одной пары x_k и x_j в матрице Х коэффициент парной корреляции >0.8, то из Х необходимо удалить x_k или x_j. Уравнение адекватно, если выполняется весь комплекс качественных условий и количественных критериев, при n 6*р. (2.21)

Исходные данные к выполнению работы приведены в табл.2.1.

Исходные данные к выполнению лабораторной работы 2

Таблица 2.1.

Динамика У (млн.ткм.) и критических факторов х₁ и х₂

У	-	x1	x2	У	-	x1	x2	У	-	x1	x2
Вариант 1	Вариант 2	Вариант 3
.?.			.?.	.?.			.?.	.?.			.?.
Вариант 4	Вариант 5	Вариант 6
.?.			.?.	.?.			.?.	.?.			.?.
Вариант 7	Вариант 8	Вариант 9
.?.			.?.	.?.			.?.	.?.			.?.
		Продолжение табл.2.1.
Вариант 10	Вариант 11	Вариант 12
.?.			.?.	.?.			.?.	.?.			.?.
Вариант 13	Вариант 14	Вариант 15
.?.			.?.	.?.			.?.	.?.			.?.
Вариант 16	Вариант 17	Вариант 18
.?.			.?.	.?.			.?.	.?.			.?.
Вариант 19	Вариант 20	Вариант 21
.?.			.?.	.?.			.?.	.?.			.?.
Вариант 22	Вариант 23	Вариант 24
.?.			.?.	.?.			.?.	.?.			.?.

Дата добавления: 2014-12-27