Лабораторная работа 4

Тема: Оптимизация использования ресурсов

Цели работы:

1. Выработка практических навыков оптимизации использования ресурсов.

2. Запуск, отладка и тестирование программы [4,c.95].

Словесная постановка задачи

Авиаремонтное предприятие располагает n видами ресурсов в количествах b_i i=1,n. Расходуя имеющиеся ресурсы, предприятие может производить m видов продукции j=1,m. Реализация 1 единицы j-й продукции дает предприятию c_j денежных единиц. На производство 1 единицы j-го продукта расходуется a_ij единиц i-го ресурса. Надо найти оптимальный план производства продукции x_j, обеспечивающий max суммарную прибыль.

Задание нa лабораторную работу

В лабораторной работе необходимо:

1. Ввести программу в ЭВМ и создать файл исходных данных.

2. Решить задачу оптимизации.

Методические рекомендации

Целевая функция задачи – максимум суммарной прибыли предприятия, имеет следующий вид 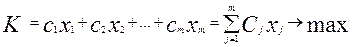. (4.1)

В процессе производства предприятие, расходуя на каждую единицу j-го вида продукции a_ij единиц i-го ресурса, не может израсходовать больше имеющегося у него запаса b_i i-го ресурса. Вышесказанное является словесным описанием ограничения задачи, математическая модель которого имеет вид

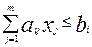при i=1,n. (4.2)

Вся произведенная продукция – реальна, то есть .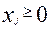

Решение поставленной задачи осуществляется по алгоритму:

Этап 1. Приведение задачи к каноническому виду, при котором:

1) все ограничения представляют собой алгебраические уравнения;

2) правые части уравнений положительны или равны 0;

3) все ;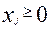

4) целевая функция максимизируется;

5) в ограничениях есть базис.

В качестве исходных данных в программу simplex.pas вводятся:

вектор коэффициентов целевой функции со своими знаками;

матрица коэффициенты ф со своими знаками;

вектор свободных членов A.

Этап 2. Заполнение симплекс-таблицы.

Этап 3. Оценка оптимальности опорного плана.

Этап 4. В случае не оптимальности плана выполняется поиск опорного столбца, опорной строки, опорного элемента и преобразование симплекс-таблицы алгоритмом Жордана-Гаусса. Если план вновь не оптимален – переходим на этап 3, если план оптимален – на этап 5.

Этап 5. Вывод результатов в файл simplex.txt.

Таблица 4.1.

Исходные данные к выполнению лабораторной работы 4

Вари-ант	Ресурс	Нормы расхода ресурсов aij x1 x2 x3 x4 x5 x6	Запасы ресурсов bj
	i=1 K ->	1.0 2.0 3.0 1.0 1.2 2.0 2.0 1.0 2.0 2.0 1.5 3.0 1.1 2.1 3.2 3.0 1.7 1.0 5.0 6.0 3.0 2.0 4.0 4.0

Продолжение табл.4.1.

	i=1 K ->	2.0 2.0 1.1 2.1 1.0 1.1 3.0 3.0 4.3 4.2 1.2 3.3 1.0 1.1 2.2 1.3 1.5 2.5 2.0 3.0 1.0 3.0 5.0 3.0
	i=1 K ->	2.0 1.0 1.0 2.0 1.1 1.1 2.0 2.0 1.0 2.0 1.1 1.2 1.2 1.1 2.2 2.1 1.2 2.3 2.0 1.0 2.0 4.0 1.0 2.0
	i=1 K ->	2.0 4.0 2.0 4.0 1.0 1.0 2.0 3.0 3.0 3.0 1.1 5.0 1.3 2.4 3.4 2.0 1.2 3.0 3.0 4.0 2.0 1.0 3.0 6.0
	i=1 K ->	2.0 2.0 1.0 4.0 1.1 2.0 3.0 1.0 2.0 2.0 1.2 3.0 2.1 3.1 1.2 2.0 1.3 1.0 2.0 3.0 4.0 2.0 5.0 2.0
	i=1 K ->	2.0 4.0 4.0 2.0 1.0 1.0 1.0 3.0 3.0 3.0 1.2 2.0 3.1 4.1 4.2 1.0 1.2 2.0 2.0 3.0 2.0 3.0 5.0 2.0
	i=1 K ->	3.0 2.0 1.0 3.0 1.2 1.0 3.0 2.0 2.0 2.0 2.5 2.0 2.1 1.1 3.2 3.0 1.7 1.0 3.4 2.3 3.1 1.5 1.0 2.1
	i=1 K ->	2.0 4.0 4.0 3.0 2.2 1.0 2.0 3.0 1.0 2.0 0.5 2.0 1.2 1.5 2.5 4.0 2.7 3.0 2.2 2.0 1.0 3.1 2.3 1.9
	i=1 K ->	2.0 1.0 2.0 2.0 2.2 1.0 3.0 2.0 3.0 3.0 2.5 2.0 1.2 2.4 1.2 2.0 2.7 3.0 3.0 4.0 2.0 3.0 2.0 1.0
	i=1 K ->	2.0 1.0 2.0 2.0 2.2 1.0 3.0 2.0 3.0 3.0 2.5 2.0 1.2 2.4 1.2 2.0 2.7 3.0 3.0 4.0 2.0 3.0 2.0 1.0
	i=1 K ->	2.0 1.0 2.0 2.0 1.5 3.0 1.0 3.0 3.0 3.0 1.6 3.0 1.2 2.2 3.4 4.0 1.3 4.0 8.0 6.0 9.0 10.0 7.0 5.0
	i=1 K ->	2.0 4.0 4.0 3.0 1.0 6.1 1.0 6.0 3.0 2.0 1.1 3.2 1.2 2.6 2.2 2.0 1.2 5.3 8.0 3.0 4.0 5.0 3.0 6.0
	i=1 K ->	2.0 1.0 2.0 3.0 1.2 2.0 1.0 3.0 1.0 1.0 1.2 1.0 1.2 2.1 3.2 3.0 1.3 1.0 9.0 4.0 5.0 3.0 1.0 3.0
	i=1 K ->	3.0 1.0 1.0 2.0 3.2 1.0 2.0 2.0 1.0 2.0 2.5 5.0 2.3 2.3 1.1 2.0 1.7 1.0 2.0 3.0 1.0 2.0 2.0 4.0

Продолжение табл.4.1.

	i=1 K ->	3.0 2.0 1.0 2.0 2.2 1.0 2.0 1.0 3.0 1.0 4.5 4.0 3.1 3.1 1.2 3.0 1.7 1.0 5.0 3.0 2.0 3.0 4.0 1.0
	i=1 K ->	1.0 2.0 1.0 2.0 3.0 2.0 1.0 3.0 2.0 1.0 2.1 2.0 2.3 2.6 2.2 3.0 3.2 2.0 6.0 4.0 5.0 3.0 3.0 2.0
	i=1 K ->	2.0 3.0 1.0 2.0 3.2 3.0 2.0 2.0 1.0 4.0 1.5 5.0 3.1 1.1 1.2 2.0 1.3 3.0 7.0 5.0 4.0 2.0 3.0 6.0
	i=1 K ->	2.0 6.0 2.0 2.0 5.2 2.0 1.0 3.0 3.0 3.0 4.5 2.0 3.1 4.1 4.2 4.0 2.7 3.0 2.0 3.0 5.0 3.0 2.0 1.0
	i=1 K ->	2.0 1.0 2.0 3.0 4.2 2.0 2.0 2.0 4.0 2.0 2.5 1.0 2.1 3.1 2.2 5.0 3.7 2.0 5.0 3.0 2.0 7.0 4.0 2.0
	i=1 K ->	2.0 1.0 3.0 2.0 1.2 2.0 1.0 3.0 1.0 2.0 2.2 1.0 1.2 2.1 3.2 3.0 1.3 1.0 9.0 4.0 5.0 4.0 2.0 3.0
	i=1 K ->	2.0 1.0 1.0 2.0 3.0 1.1 1.0 2.0 1.0 2.0 3.5 5.2 2.3 2.3 1.4 2.0 1.7 1.3 1.0 2.0 3.0 2.0 3.0 4.0
	i=1 K ->	1.0 2.0 1.0 2.0 2.2 1.0 2.0 1.0 3.0 1.0 4.5 4.0 2.1 2.1 1.2 3.0 1.7 1.0 5.0 3.0 2.0 4.0 5.0 1.0
	i=1 K ->	1.0 2.0 1.0 2.0 4.0 2.0 1.0 3.0 2.0 1.0 2.1 2.0 2.3 2.6 2.2 3.0 1.2 2.0 6.0 4.0 3.0 3.0 2.0 2.0
	i=1 K ->	2.0 3.0 2.0 2.0 3.2 3.0 2.0 2.0 1.0 4.0 2.5 5.0 3.1 1.1 1.3 2.0 1.3 4.0 7.0 5.0 3.0 3.0 2.0 4.0

Дата добавления: 2014-12-27