
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лабораторная работа 3
|
|
|
|
Тема: Поиск ложной информации
Цели работы:
1. Выработка практических навыков оценки закона распределения
случайной величины и определения наличия ложной информации.
2. Запуск, отладка и тестирование программы.
3. Оценка наличия ложной информации с помощь программы [4,c.45].
Словесная постановка задачи
Имеется массив X1={хi} наблюдений о временах обслуживания ВС. Необходимо оценить наличие ложной информации в {хi} путем оценки вида закона распределения Х.
Задание нa лабораторную работу
В лабораторной работе необходимо:
1. Ввести программу в ЭВМ и создать файл исходных данных.
2. Оценить закон распределения Х программой fu_ras.pas.
3. Дать заключение об отсутствии или наличии ложной информации.
Методические рекомендации
Решение поставленной задачи осуществляется по алгоритму:
Шаг 1. Вычислить точечную оценку математического ожидания случайной величины 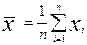 , (3.1)
, (3.1)
где n - объем выборки; хi - i-e наблюдение случайной величины (i=1,n).
Шаг 2. Определить точечную оценку дисперсии 
 (3.2)
(3.2)
и среднеквадратического отклонения 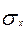 случайной величины X.
случайной величины X.
Шаг 3. Вычислить оценки 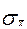 и
и 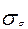
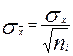 и
и 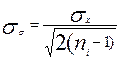 (3.3)
(3.3)
Шаг 4. Определить интервальную оценку математического ожидания 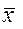
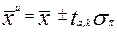 (3.4)
(3.4)
где 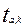 - теоретическое значение квантиля критерия Стьюдента табл.1[1] либо как
- теоретическое значение квантиля критерия Стьюдента табл.1[1] либо как  (3.5)
(3.5)
при k = n-1 и доверительной вероятности ά = 0.95, входах в табл.1 [1]
Шаг 5. Определить количество интервалов nи, на которое необходимо
разбить статистический ряд значений случайной величины
nи = 5 log(n), (3.6)
где n - число наблюдений случайной величины Х.
Шаг 6. Вычислить размер интервала разбиения статистического ряда
значений случайной величины X
 , (3.7)
, (3.7)
где 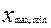 - максимальное и минимальное значения случайной величины.
- максимальное и минимальное значения случайной величины.
Шаг 7. Определить количества попаданий значений случайной величины в каждый интервал ni i=1,m.
Шаг 8. Вычислить вероятности попадания в i-й интервал  . (3.8)
. (3.8)
Шаг 9. Проверить условие для каждого интервала n p*i > 5. Если для i-го интервала условие не выполняется, его объединяют с (i-1) -м интервалом.
Шаг 10. Определить значения функции распределения F*(х) по статистическим значениям выборки наблюдений
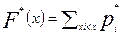 . (3.9)
. (3.9)
Шаг 11. Вычислить значения функции плотности распределения
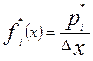 . (3.10)
. (3.10)
Шаг 12. Построить гистограммы для F*(х) и f*(х).
Шаг 13. Сформировать гипотезу Ho о принадлежности выборки значений случайной величины к одному из законов распределения (табл.3.1).
Шаг 14. Для гипотетического закона распределения определить точечные оценки расчетных параметров и значений Fтi (х).
Таблица 3.1.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 241; Нарушение авторских прав?; Мы поможем в написании вашей работы!