Наращение и дисконтирование по сложным процентным ставкам

. Наращение по сложным процентам можно представить как последовательное реинвестирование средств, вложенных под простые проценты на один период начисления. Присоединение начисленных процентов к сумме, которая послужила базой для их начисления, часто называют капитализацией процентов.

Начисление по сложному проценту осуществляется по следующей формуле:

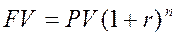
(15)

где n - число лет;

r – ставка процента;

(1+r)ⁿ - множитель наращения по сложным процентам.

Значения этого множителя для целых чисел n приводятся в таблицах сложных процентов.

Использование в расчетах сложного процента более логично, поскольку в этом случае капитал, генерирующий доходы, постоянно возрастает. Инвестиции на условиях сложного процента более выгодны.

Для операций финансового анализа существуют специальные таблицы шести функций:

1 – будущая стоимость единицы

2 – накопление единицы за период

3 – фактор фонда возмещения

4 – текущая стоимость единицы

5 – текущая стоимость единичного аннуитета

6 – взнос на амортизацию единицы

Рассмотрим логику построения таблиц шести функций

1. Будущая стоимость единицы (колонка 1)

Показывает, какая сумма будет накоплена на счете к концу определенного периода при заданной ставке дохода, если сегодня положить на счет 1 денежную единицу

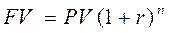
(16)

2. Накопление единицы за период (колонка 2)

Показывает, какая сумма будет накоплена на счете при заданной ставке, если регулярно в течение определенного периода откладывать на счет 1 денежную единицу.

Серия равновеликих платежей отстающих друг от друга на один и тот же промежуток времени называется аннуитетом или финансовой рентой. По моменту выплаты аннуитетные платежи подразделяются на обычные (постнумерандо), которые производятся в конце соответствующих периодов (года, месяца), и авансовые (постнумерандо), которые производятся в начале этих периодов.

3. Фактор фонда возмещения

Показывает, сколько нужно откладывать на счет регулярно в течение определенного времени, чтобы при заданной ставке дохода иметь на счете к концу этого срока определенную сумму денег.

4. Текущая стоимость единицы

Показывает, какова при заданной ставке дисконта текущая стоимость 1 денежной единицы, получаемой в конце определенного периода времени

5. Текущая стоимость единичного аннуитета

Показывает, какова при заданной ставке дисконта текущая стоимость серии платежей в 1 денежную единицу в течение определенного периода.

6. Взнос на амортизацию единицы

Показывает, какими должны быть аннуитетные платежи в счет погашения кредита, выданного на определенный период под определенный процент.

В современных условиях проценты капитализируются, как правило, не один, а несколько раз в году – по полугодиям, кварталам, месяцам. Некоторые зарубежные банки практикуют даже ежедневное начисление процентов. На практике, как правило, фиксируется не ставка за период начисления, а годовая ставка, одновременно указывается период начисления процентов

Различными видами финансовых контрактов могут предусматриваться различные схемы начисления процентов. Чтобы обеспечить сравнительный анализ эффективности таких контрактов применяется действительная или эффективная ставка процента. Это ставка – универсальная для любой схемы начисления процентов и измеряет тот реальный относительный доход, который получают в целом за год. То есть, эффективная ставка – это годовая ставка сложных процентов, которая дает тот же результат, что и m – разовое начисление процентов по ставке r/m. Эффективная ставка (r(e)) зависит от количества внутригодовых начислений, причем с ростом m она увеличивается. Эффективную ставку можно определить по формуле:

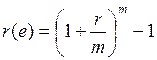
(17)

Дата добавления: 2014-12-27