Теорема. Закон больших чисел и центральная предельная

Закон больших чисел и центральная предельная

Под законом больших чисел в теории вероятности понимается ряд теорем, в каждой из которых устанавливается факт асимптотического приближения среднего значения большого числа опытных данных к математическому ожиданию случайной величины. Таким образом, при определённых условиях, суммарное поведение достаточно большого числа случайных величин становится закономерным.

В основе доказательств этих теорем лежит Неравенство Чебышёва, установленное известным русским математиком Пафнутием Львовичем Чебышёвым.

Неравенство Чебышёва справедливо для дискретных и непрерывных случайных величин. Для простоты, ограничимся доказательством этого неравенства для дискретных величин.

Рассмотрим дискретную случайную величину Х, заданную законом распределения:

X			…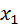
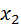
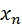
P			…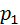

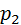
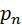
Поставим задачу: Оценить вероятность того, что отклонение случайной величины Х от её математического ожидания М(Х) не превышает по абсолютной величине число ε > 0. Если ε достаточно мало, то мы оценим, таким образом, вероятность того, что Х примет значения, достаточно близкие к своему математическому ожиданию.

Неравенство Чебышёва: Вероятность того, что отклонение случайной величины Х от её математического ожидания по абсолютной величине меньше положительного числа ε, не меньше, чем величина 1 :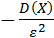

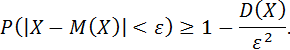
Доказательство: Пусть Х – дискретная случайная величина. Воспользуемся формулой вероятности противоположного события: 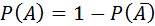. Тогда имеем:

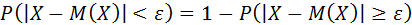(1)

Узнаем, чему равна вероятность 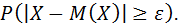Рассмотрим определение дисперсии дискретной случайной величины:

.

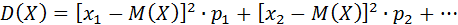
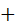
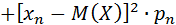Все слагаемые этой суммы неотрицательны. Отбросим те слагаемые, у которых 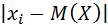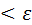(для оставшихся слагаемых 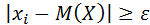), вследствие чего сумма только уменьшится.

Условимся считать, для определённости, что отброшено k первых слагаемых. Не нарушая общности, можно считать, что в таблице распределения возможные значения занумерованы именно в таком порядке.

Таким образом, получаем неравенство:

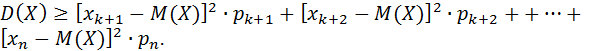(2)

Рассмотрим неравенства для оставшихся слагаемых:

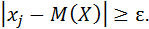
Так как обе части таких неравенств положительны, возведем в квадрат:

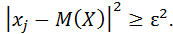
Заменяя в формуле (2) каждый из множителей 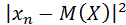числом ε (при этом неравенство может лишь усилиться), получаем:

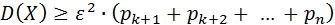(3)

Сумма 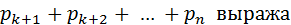ет вероятность того, что Х примет одно, безразлично какое, из значений 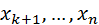. А при любом из них отклонение удовлетворяет неравенству 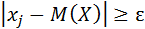, следовательно, имеем:

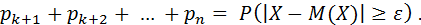
Из формулы (3) получаем:

<=>

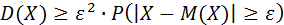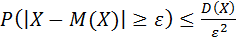<=> (4)

Подставляя результат (4) в выражение (1), окончательно получим:

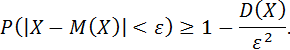
Теорема Чебышёва: Если 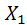, , 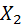…, 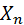– попарно независимые случайные величины, причём дисперсии их равномерно ограничены (не превышают постоянного числа С), то, как бы мало ни было положительное число ε, вероятность неравенства

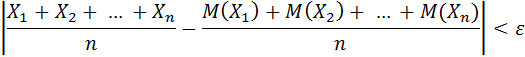
будет как угодно близка к единице, если число случайных величин достаточно велико.

Другими словами, в условиях теоремы, имеем:

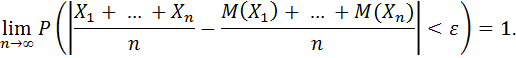
Доказательство: Рассмотрим По свойствам математического ожидания имеем:

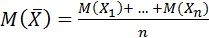. (1)

Применяя к неравенство Чебышёва, получаем:

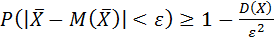(2)

Согласно условию теоремы и свойствам дисперсии имеем:

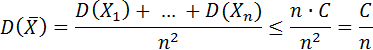
Подставим этот результат в неравенство (2) (неравенство может лишь усилиться):

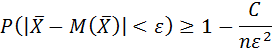
Тогда

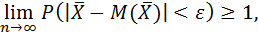
но, так как вероятность не может превышать единицу, то имеем:

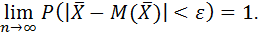
Теорема Чебышёва утверждает, что если рассматривается достаточно большое число независимых случайных величин, имеющих равномерно ограниченные дисперсии, то почти достоверным можно считать событие, состоящее в том, что отклонение среднего арифметического случайных величин от среднего арифметического их математических ожиданий будет по абсолютной величине сколь угодно малым.

Следствие из теоремы Чебышёва (частный случай теоремы): Если 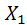, …, 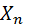– попарно независимые случайные величины, имеющие одно и то же математическое ожидание а, и если дисперсии этих величин равномерно ограничены, то, как бы мало ни было число ε >0, вероятность неравенства

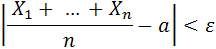
будет как угодно близка к единице, если число случайных величин достаточно велико.

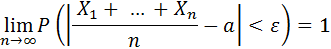
Заметим, что теорема Чебышёва справедлива как для дискретных, так и для непрерывных случайных величин.

Сущность теоремы Чебышёва: Среднее арифметическое достаточно большого числа независимых случайных величин (дисперсии которых равномерно ограничены) утрачивает характер случайной величины.

Значение теоремы Чебышёва для практики: Теорема Чебышёваустанавливает связь между теорией вероятностей, которая рассматривает средние характеристики всего множества значений случайной величины, и математической статистикой, оперирующей ограниченным множеством значений этой величины. Она показывает, что при достаточно большом числе измерений некоторой случайной величины среднее арифметическое значение этих измерений приближаются к математическому ожиданию.

Теперь познакомимся с теоремой Бернулли.

Теорема Бернулли была опубликована в 1713 году, получила название «закона больших чисел» и положила начало теории вероятностей как науке. Доказательство Бернулли было сложным. Простое доказательство было дано П.Л. Чебышёвым в 1846 году.

Теорема Бернулли: Если в каждом из n независимых испытаний вероятность р появления события А постоянна, то как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности р по абсолютной величине будет сколько угодно малым, если число испытаний достаточно велико.

Другими словами, если ε >0 – сколько угодно мало, то, при

соблюдении условий теоремы, имеет место равенство:

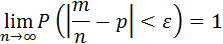
Доказательство: Пусть 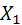– дискретная случайная величина, число появлений события А в первом испытании, 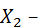во втором испытании, и т. д., 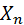– в n -ом испытании.

Ясно, что закон распределения вероятностей каждой случайной величины имеет вид:

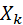
	0	1
Р	1-р	р

∀

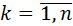
Т.к. испытания независимы, то и величины 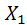, …, 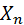попарно независимы, их дисперсии ограничены. Действительно, дисперсия каждой величины 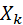( 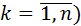равна pq. Т.к. p + q=1,то pq ≤ . Поясним это подробнее. Произведение двух сомножителей, сумма которых постоянна, имеет наибольшее значение при равенстве сомножителей. Т.к. p + q = 1, то при p = q = получаем: pq ≤ 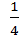. Применяя теорему Чебышёва (а точнее, ее частный случай), получим:

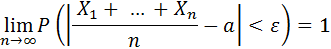
Так как а = р для любой рассматриваемой нами случайной величины, то

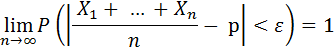
Докажем, что среднее арифметическое наших случайных величин равно относительной частоте появлений события А в испытаниях:

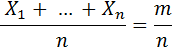
Так как каждая из величин , …, 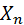при появлении события А в соответствующем испытании принимает значение, равное единице, то 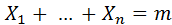, где 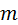– число появления события в n испытаниях. Тогда получаем:

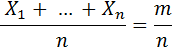
Учитывая это равенство, окончательно получим то, что требовалось доказать:

.

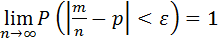Теорема Бернулли утверждает, что при n →∞ относительная частота стремится по вероятности к р.

Теорема Бернулли объясняет, почему относительная частота при достаточно большом числе испытаний обладает свойством устойчивости и оправдывает статистическое определение вероятности.

Теперь познакомимся с Центральной предельной теоремой, которую представил и доказал выдающийся русский математик А.М.Ляпунов, ученик П.Л. Чебышёва. Сформулируем ее в общем виде.

Центральная предельная теорема (Теорема Ляпунова): Если случайная величина X представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то Х имеет распределение, близкое к нормальному.

Пример: Допустим, определяется некоторый экономический показатель, например, потребление электроэнергии в городе за год. Величина суммарного потребления складывается из потребления энергии отдельными потребителями, которое имеет случайные значения с разными распределениями. Теорема утверждает, что в этом случае, какое бы распределение ни имели отдельные составляющие, распределение результирующего потребления будет близко к нормальному. Но, при усилении влияния отдельных факторов, могут появляться отклонения от нормального распределения результирующего параметра, например, может возникать асимметрия или эксцесс. Поэтому на практике следует проверить экспериментально гипотезу о нормальном распределении.

Рассмотрим подробнее оценку отклонения теоретического распределения от нормального.

Определение: Эмпирическим называется распределение относительных частот.

Эмпирические распределения изучает математическая статистика.

Определение: Теоретическим называется распределение вероятностей.

Теоретические распределения изучает теория вероятностей.

Определение: Асимметрией теоретического распределения называется отношение центрального момента третьего порядка к кубу среднего квадратического отклонения:

=

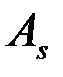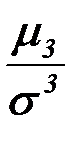
Заметим, что если «длинная часть» кривой распределения расположена правее моды (точки максимума функции плотности), то 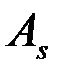> 0, а если – слева, 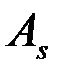< 0.

f(х) f(x)

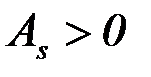
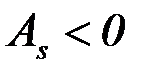
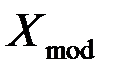х х

Определение: Эксцессом теоретического распределения называют характеристику, которая определяется равенством:

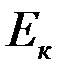= - 3.

Заметим, что для нормального распределения асимметрия и эксцесс равны нулю.

Если 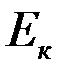> 0, то кривая имеет более высокую и «острую» вершину, чем нормальная кривая. Если 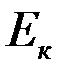< 0, то кривая имеет более низкую и «плоскую» вершину, чем нормальная кривая.

f(x) f(x)

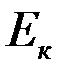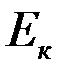> 0 < 0

0 x 0 х

Нормальная кривая изображена пунктирной линией. При этом предполагается, что нормальное и теоретическое распределения имеют одинаковые математические ожидания и дисперсии.

Если асимметрия и эксцесс имеют небольшие значения, то можно предположить близость данного распределения к нормальному. Большие значения асимметрии и эксцесса указывают на значительное отклонение от нормального распределения.

Практическое значение теоремы Ляпунова: Обычно уже при конечном, но достаточно большом числе слагаемых, закон распределения суммы нескольких случайных величин принимают за нормальный закон (складываемые случайные величины должны быть равнозначны в общей сумме: ни одна из них не должна занимать явно преимущественного места по сравнению с другими величинами).

Пример: Дано n приближенных чисел, округленных до единицы. Погрешность каждого из них есть случайная величина, распределенная равномерно на участке от -0,5 до +0,5 с математическим ожиданием a = 0 и D(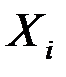) = 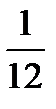. Найдем закон распределения суммы этих чисел. По теореме Ляпунова будем считать, что закон распределения суммы – нормальный. Тогда:

М (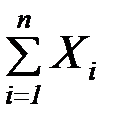) = 0, D (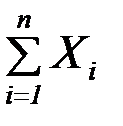) = 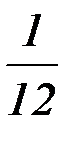n, .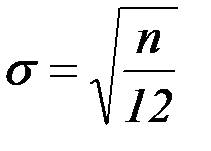

Найдем плотность распределения вероятностей:

f(x) = · = · .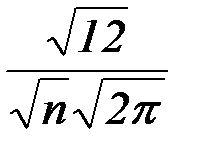

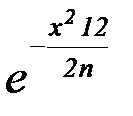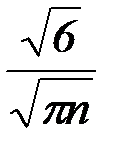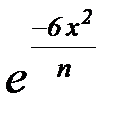Дата добавления: 2014-12-27