
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Условные распределения
|
|
|
|
Вычисление основных числовых характеристик
случайных величин Х и Y.
Основные числовые характеристики случайных величин Х и Y, являющихся компонентами двумерной случайной величины 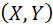 вычисляют по формулам, данным для одномерных случайных величин. Сделаем сводку этих формул.
вычисляют по формулам, данным для одномерных случайных величин. Сделаем сводку этих формул.
Если 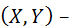 двумерная случайная величина дискретного типа, и она задана таблицей совместного распределения Х и Y:
двумерная случайная величина дискретного типа, и она задана таблицей совместного распределения Х и Y:
| Y \ Х | 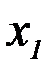
| 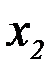
| … | 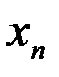
|
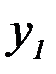
| 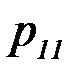
| 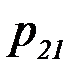
| … | 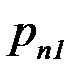
|
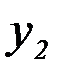
| 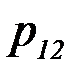
| 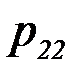
| … | 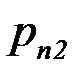
|
| … | … | … | … | … |
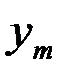
| 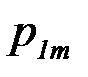
| 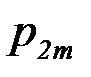
| … | 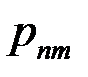
|
Тогда имеем:
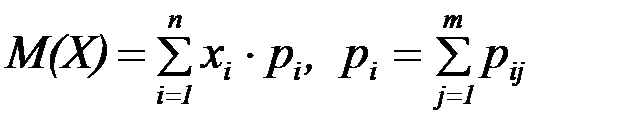
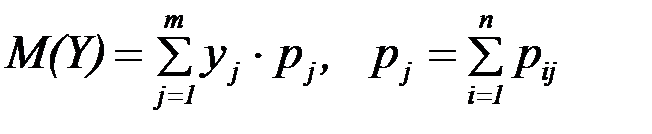
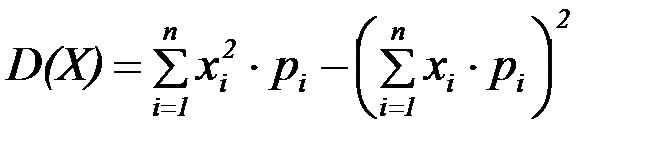
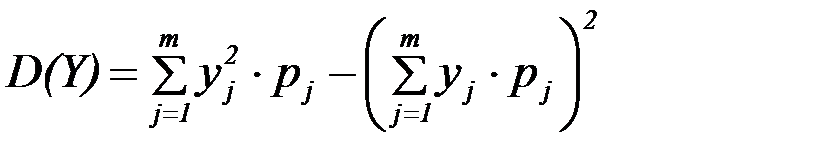
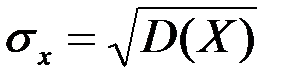
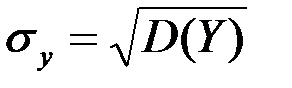
Если 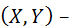 двумерная случайная величина непрерывного типа, и она задана плотностью f(x,y) совместного распределения вероятностей Х и Y, тогда имеем:
двумерная случайная величина непрерывного типа, и она задана плотностью f(x,y) совместного распределения вероятностей Х и Y, тогда имеем:
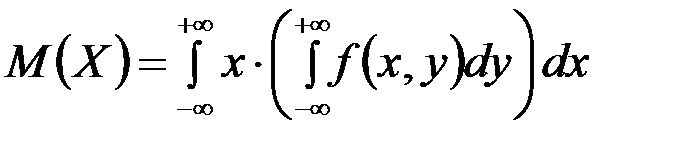
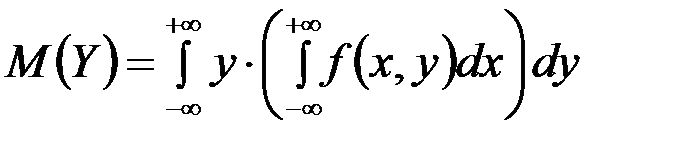
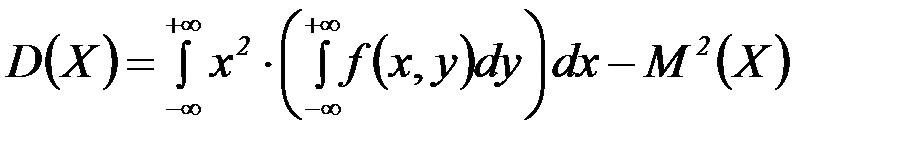
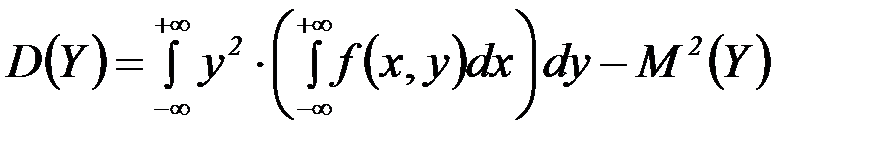

Как известно, вероятность совместного появления дискретных случайных величин 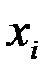 ,
, 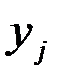 можно выразить в виде:
можно выразить в виде:
р( 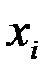 ,
, 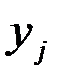 ) = р(
) = р( 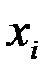 )р(
)р(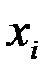 /
/ 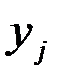 ),
),
где р(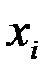 /
/ 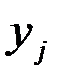 ) – условная вероятность.
) – условная вероятность.
Определение: Условным распределением компоненты Х при Y = 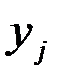 называют совокупность условных вероятностей р(
называют совокупность условных вероятностей р(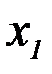 /
/ 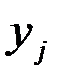 ), р(
), р(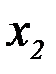 /
/ 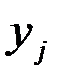 ), …, р(
), …, р(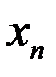 /
/ 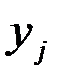 ), вычисленных в предположении, что событие Y =
), вычисленных в предположении, что событие Y = 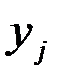 (j имеет одно и то же значение при всех значениях Х) уже наступило.
(j имеет одно и то же значение при всех значениях Х) уже наступило.
Аналогично определяется условное распределение компоненты Y.
Определение: Условной плотностью 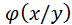 распределения вероятностей компоненты Х при данном значении
распределения вероятностей компоненты Х при данном значении 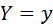 называется отношение плотности совместного распределения вероятностей
называется отношение плотности совместного распределения вероятностей 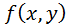 двумерной случайной величины
двумерной случайной величины 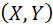 к плотности совместного распределения вероятностей
к плотности совместного распределения вероятностей 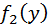 компоненты
компоненты 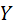 :
:
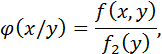
или
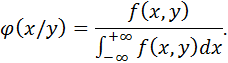
Заметим, что отличие условной плотности 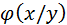 от безусловной плотности
от безусловной плотности 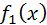 состоит в том, что функция
состоит в том, что функция 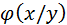 даёт распределение
даёт распределение 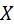 при условии, что компонента
при условии, что компонента 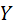 приняла значение
приняла значение 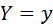 . Функция же
. Функция же 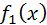 даёт распределение
даёт распределение 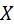 независимо от того, какие из возможных значений приняла компонента
независимо от того, какие из возможных значений приняла компонента 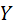 .
.
Аналогично определяется условная плотность компоненты 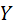 при данном значении
при данном значении 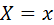 :
:
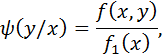
или
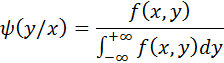
Свойства 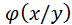 и
и 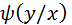 аналогичны свойствам функции плотности.
аналогичны свойствам функции плотности.
Определение: Условным математическим ожиданием дискретной случайной величины 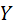 при
при 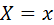 (x – определённое возможное значение X), называют сумму произведений возможных значений
(x – определённое возможное значение X), называют сумму произведений возможных значений 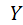 на их условные вероятности:
на их условные вероятности:
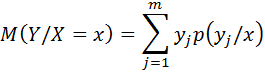
Определение: Условным математическим ожиданием непрерывной случайной величины 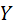 при
при 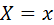 (x – определённое возможное значение X), называют несобственный интеграл от произведения
(x – определённое возможное значение X), называют несобственный интеграл от произведения 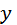 на условная плотность
на условная плотность 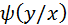 при
при 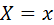 :
:
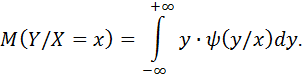
Определение: Условное математическое ожидание 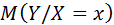 (краткое обозначение
(краткое обозначение 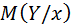 ) есть функция от
) есть функция от 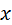 :
:
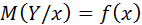 ,
,
которую называют функцией регрессии 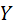 на
на 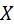 .
.
Аналогично определяются у словное математическое ожидание случайной величины 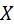 и функция регрессии
и функция регрессии 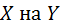 :
:
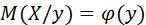 .
.
Задавая различные значения 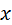 , можно построить кривую регрессии
, можно построить кривую регрессии 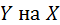 .
.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 1040; Нарушение авторских прав?; Мы поможем в написании вашей работы!