
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определение предельных размеров частиц веществ с неразрушенными полимерными молекулами
|
|
|
|
Расчет максимального наноразмера на основании уравнения Шредингера
Рассмотрим наночастицу, для которой справедливо уравнение Шредингера:
 . (2.56)
. (2.56)
Для изотропной частицы (одномерный случай):
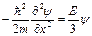 , (2.57)
, (2.57)
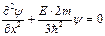 , (2.58)
, (2.58)
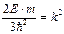 , (2.59)
, (2.59)
 , (2.60)
, (2.60)
 , (2.61)
, (2.61)
 . (2.62)
. (2.62)
Величина  определяет размер решетки, когда на любую ячейку оказывают все остальные, в том числе и центральная ячейка. Следовательно, при таком размере частиц она ведет себя при соответствующих внешних воздействиях не так как обычный (макро-) кристалл, в котором его размерами можно пренебречь так как размерные эффекты (то есть какие-либо зависимости свойств от размера) отсутствуют. Следовательно, в формуле (2.62) можно принять
определяет размер решетки, когда на любую ячейку оказывают все остальные, в том числе и центральная ячейка. Следовательно, при таком размере частиц она ведет себя при соответствующих внешних воздействиях не так как обычный (макро-) кристалл, в котором его размерами можно пренебречь так как размерные эффекты (то есть какие-либо зависимости свойств от размера) отсутствуют. Следовательно, в формуле (2.62) можно принять  и, как видно из условия (2.62) получили размерную границу наночастиц
и, как видно из условия (2.62) получили размерную границу наночастиц  полностью тождественную формулам, выведенным ранее (см. (2.21), (2.50), (2.55)).
полностью тождественную формулам, выведенным ранее (см. (2.21), (2.50), (2.55)).
При исследовании свойств наноразмерных объектов, в основном, уделяется внимание кристаллическим, в большинстве случаев моноэлементным (например, металлы) или биэлементным (полупроводники, оксиды, сульфиды) веществам [1-5]. В то же время за последние годы появились исследования свойств наноразмерных частиц полимерных веществ, которые в большинстве случаев создаются либо методами диспергирования фрагментов полимерного вещества при низкой температуре [16], либо измельчением на специальных экструдерах. Как показано в некоторых работах, введение таких частиц в однородную полимерную матрицу может привести к изменению некоторых ее характеристик в зависимости от их концентрации и размера [16-23].
Критический размер наночастицы  можно определить по формуле:
можно определить по формуле:
 .
.
Уравнение (2.23) для расчета дебаевской температуры можно переписать в виде
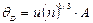 , (2.63)
, (2.63)
где А – постоянная величина, равная
 . (2.64)
. (2.64)
В полимерную молекулу обычно входят атомы О(16), N(14), C(12), H(1) (в скобках указаны массовые числа, измеренные в атомной единице массы – а.е.м). Кроме указанных атомов, в состав полимеров могут входить и другие, например, атомы серы, фосфора, кремния и некоторых металлов. Однако их концентрация обычно невелика и поэтому для получения оценочных значений  для полимеров примем среднюю массу атома, равную 10 а.е.м, то есть
для полимеров примем среднюю массу атома, равную 10 а.е.м, то есть 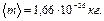 если плотность вещества равна r, а средняя масса атома есть
если плотность вещества равна r, а средняя масса атома есть  , то атомная плотность (n в формуле (2.63)) равна:
, то атомная плотность (n в формуле (2.63)) равна:
 (2.65)
(2.65)
Плотность полимеров изменяются в достаточно широком интервале, в частности, от 920 кг/м3 (полиэтилен) до 1800 кг/м3 (полихлорвинил). Для расчетов примем среднее значение плотности r =12,00 кг/м3. В этом случае
 (2.66)
(2.66)
то есть условие (2.63) примет вид:
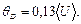 (2.67)
(2.67)
Скорость звука в полимерных материалах зависит от состава и изменяется, например, от 2400 м/с для эбонита до 5000 м/с для древесины (сосна). Следовательно, значение расчетной характеристической температуры для большинства полимерных материалов находится в интервале (см. условие (2.67)):
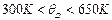 , (2.68)
, (2.68)
или

Таким образом, размерная граница между наносостоянием и объемной фазой полимерных материалов находится в интервале
 . (2.69)
. (2.69)
Учитывая большое многообразие полимеров можно расширить этот интервал и представить его в виде:
 .
.
В этот интервал кроме частиц полимерных материалов попадают частицы практически всех металлов [2-5], галогенидов, полупроводников типа 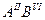 и
и 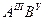 [1-5, 15, 17], и других веществ, например, оксидов, сульфидов и т. д. Отсюда следует, что наносвойства частиц полимера могут проявляться при размерах
[1-5, 15, 17], и других веществ, например, оксидов, сульфидов и т. д. Отсюда следует, что наносвойства частиц полимера могут проявляться при размерах  . Наименьшее значение величины
. Наименьшее значение величины  соответствует для частиц полимера с максимальной скоростью распространения звука, максимальным значением числа атомов в единице объема и, с большой вероятностью равное
соответствует для частиц полимера с максимальной скоростью распространения звука, максимальным значением числа атомов в единице объема и, с большой вероятностью равное 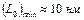 .
.
Другими словами, при размере r > 13 нм частицы будут обладать свойствами характерными для вещества с большим объемом (объемными свойствами), то есть размерный фактор не будет играть значительную роль. Однако, возможны и такие случаи, когда наносвойства будут проявляться и при значениях 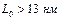 , но при r<9 нм размерный эффект будет всегда иметь место, т. е. при r<9 нм любая полимерная частица с очень высокой вероятностью будет обладать свойствами наночастицы которые будут отличаться от соответствующих свойств объемного аналога.
, но при r<9 нм размерный эффект будет всегда иметь место, т. е. при r<9 нм любая полимерная частица с очень высокой вероятностью будет обладать свойствами наночастицы которые будут отличаться от соответствующих свойств объемного аналога.
Следует подчеркнуть, что рассмотренные выше рассуждения могут быть с большой точностью применены для различного состава веществ. Для этого необходимо знать значения скорости звука и объемной атомной плотности, что позволит использовать для изучаемого вещества показатели  и n при расчете
и n при расчете  (см. формулу 2.69). Если вещество анизотропное, то формула (2.66) примет вид:
(см. формулу 2.69). Если вещество анизотропное, то формула (2.66) примет вид:
 (2.70)
(2.70)
где  – скорость звука для направления
– скорость звука для направления  ,
,  – средняя линейная атомная плотность вдоль направления, определяемого вектором
– средняя линейная атомная плотность вдоль направления, определяемого вектором  , то есть
, то есть  – это усредненное число атомов на единице длины вдоль направления
– это усредненное число атомов на единице длины вдоль направления  .
.
При диспергировании полуфабриката полимерных веществ до размеров их частиц в несколько десятков нанометров зачастую требуется ответить на вопрос, есть ли в полученной частице хотя бы одна молекула исходного вещества, оставшаяся неразрушенной, так как при диспергировании как правило, происходит разрушение молекул полимера с образованием радикальных продуктов различной массы. Для ответа на этот вопрос необходимо учесть следующие соображения.
Пусть имеется полимерная молекула, линейный размер который равен r, а химический состав определяется формулой 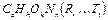 , где C, H, O, N – атомы углерода, водорода, кислорода, азота соответственно,
, где C, H, O, N – атомы углерода, водорода, кислорода, азота соответственно, 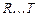 – атомы других элементов, которые входят в ее состав. Нижний индекс в формуле указывает на число соответствующих атомов в молекуле полимера.
– атомы других элементов, которые входят в ее состав. Нижний индекс в формуле указывает на число соответствующих атомов в молекуле полимера.
Для того, чтобы утверждать, что в дисперсной частице вещества имеется хотя бы одна «неразорванная» при диспергировании частиц полуфабриката полимерная молекула полимера, размер дисперсионной частицы R должен удовлетворять условию:
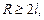 (2.71)
(2.71)
где l – длина линейной молекулы.
Очевидно, что при сохранении линейной конфигурации полимерных молекул в частице с размером D<l вероятность наличия не разрушенной полимерной молекулы равна нулю.
Следовательно, если размер полимерной молекулы равен l, и эта молекула сохраняет линейную структуру, то вероятность присутствия в частице с размером R хотя бы одной неразрушенной молекулы описывается зависимостью P(R), приведенной на рис. 2.5.
В блоке полимера, как и в полученной из него при диспергировании частице, полимерная молекула может иметь конфигурацию глобулы. Причем, это «сворачивание» макромолекулы (образование глобулы) может происходить в процессе измельчения объемных частиц полимера, так как с увеличением удельной поверхности частицы увеличивается и поверхностная энергия, что может привести к образованию сферолитов. Известно, что с глобулярной структурой вещество обладает свойствами отличными от тех, которыми вещество обладает при линейной укладке его молекул. Но процесс такого изменения расположения атомов в молекуле обусловлен размерным фактором и, следовательно, может сопровождаться появлением нанофазы. Размер образовавшейся глобулы (G) определяет минимальный размер частицы полимера, в которой может быть неразрушенная молекула.
Если состав полимерной молекулы (S) представить в виде суммы 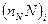
 (2.72)
(2.72)
где N – название I –того элемента, 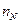 - число этих атомов в молекуле, K – число атомов различного типа в молекуле, то суммарный объем всех атомов в полимерной молекуле, W в рамках модели шаровой упаковки атомов, можно определить условием:
- число этих атомов в молекуле, K – число атомов различного типа в молекуле, то суммарный объем всех атомов в полимерной молекуле, W в рамках модели шаровой упаковки атомов, можно определить условием:
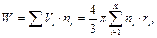 (2.73)
(2.73)
где  - размер атома i -того типа,
- размер атома i -того типа,  – валентный радиус атома i- того типа.
– валентный радиус атома i- того типа.
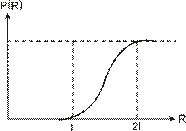
Рисунок 2.5 – Зависимость вероятности P(R) наличия в частице размером R хотя бы одной линейной молекулы длиной l
Для определения объема полимерной глобулы, образованной из одной полимерной молекулы, можно использовать представления о плотнейшей шаровой упаковке. Хотя в полимерной молекуле атомы имеют разные размеры, а форма атомов (точнее их электронных орбиталей), пусть и незначительно, но отличается от сферической, тем не менее, можно, на наш взгляд, для описания глобулы применить модель плотнейшей шаровой упаковки. Коэффициент упаковки (или коэффициент компактности), определяемый как отношение объема всех шаров в молекуле к объему, занимаемому самой молекулой, равен 0,74, то есть наименьший объем глобулы молекулы (V) при плотнейшей упаковке атомов в ней равен:
 (2.74)
(2.74)
Из выражения (2.74) значение G определяется условием:
 (2.75)
(2.75)
Таким образом, для полимеров любых типов с известным составом их молекулы и радиусами атомов (r) (см. 2.73) необходимо из выражений (2.75) рассчитать величину 2l и G. Если R – размер частицы, то вероятность того, что в этой частице присутствует хотя бы одна неразрушенная молекула 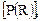 определяется условием:
определяется условием:
 , (2.76)
, (2.76)
причем функция P(R) должна быть такой, чтобы существовали ее производные 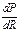 в точках R=G и R=2l. Например, в качестве такой функции
в точках R=G и R=2l. Например, в качестве такой функции 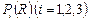 могут быть выбраны функции вида:
могут быть выбраны функции вида:
 . (2.77)
. (2.77)
При этом выполняется условие как непрерывности функции
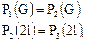 (2.78)
(2.78)
так и ее производной. Если процесс глобулизации при экструзии (ли любом другом методе измельчения частиц) отсутствует, то G=l.
Рассмотренная методика может применяться для определения размерной границы между наносостоянием и объемными свойствами  не только для частиц полимеров. Но и частиц любых веществ, химический состав которых известен, что определяет значение (n) (см. 2.77), а также в том случае, когда известна скорость звука (U) в этом веществе. В этом случае можно рассчитать значение дебаевской температуры
не только для частиц полимеров. Но и частиц любых веществ, химический состав которых известен, что определяет значение (n) (см. 2.77), а также в том случае, когда известна скорость звука (U) в этом веществе. В этом случае можно рассчитать значение дебаевской температуры  и затем значение
и затем значение 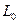 .
.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 585; Нарушение авторских прав?; Мы поможем в написании вашей работы!