Физические предпосылки к оценке наноразмерности частиц

Критерии оценки наноразмерности

Сложившаяся в настоящее время практика оценки геометрической величины наночастицы ста нанометрами (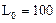 нм) [1-4], на наш взгляд, совершенно не приемлема с научной точки зрения по ряду причин.

Во-первых, значение нм совершенно ничем не обосновано кроме того, разве, что . Но с таким же успехом можно было бы взять 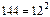или 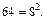Отметим, что в книге [5] уже говориться о 10 нм как о типичном размере нанообъектов. Геометрическая (размерная) граница, определяющая максимальный размер наночастицы, по общему мнению, не является резкой (точной) и напоминает по смыслу температуру застекловывания или затвердевания, например, олигомеров или полимеров. Но вряд ли найдется такой «исследователь», который бы предложил считать температуру затвердевания всех стеклообразных тел и кристаллизации полимеров равной 625 К, потому что 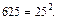С таким же «успехом» можно предложить единую температуру плавления или кристаллизации, например, 2500 К, единый размер атома 1,0 Ǻ и т. д.

Во-вторых, это значение считается одинаковым для всех типов веществ, хотя многочисленные экспериментальные данные, приведенные в научной литературе [2-7] и отражающие зависимость значений параметра какого-либо свойства от размера частиц этого не подтверждают. Типичная кривая зависимости величины экспериментальных параметров от крупности вещества приведена на рис. 2.1. При вещество относится к объемной фазе у которой размерные эффекты отсутствуют, то есть параметры вещества 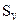не зависят от размера объекта. При 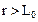- вещество является нанообъектом и характеристики его свойств отличаются от объемных. Наносвойства и объемные свойства выражены тем в большей степени, чем сильнее указанные выше неравенства ( 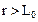или 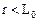). Именно такие зависимости ряда физических свойств от размеров наблюдаются экспериментально [3-10], причем переход от объемных значений одинаковых параметров к параметрам наноразмерным ( на рис. 2.1) для одних и тех же физических свойств неодинаков для различных веществ.

В-третьих, оценка наноразмерности в 100 нм неприемлема еще и потому, что экспериментальные результаты многочисленных исследований соответствуют значениям для широкого круга веществ значениям, не превышающим 30 нм, то есть 100 нм для этих частиц это уже объемная фаза. Например, при изучении структуры кристаллов методом дифракции быстрых электронов толщина образцов для метода «на просвет», равная 100 нм является настолько большой, что затрудняет получение качественной дифракционной картины. Частица размером 100 нм включает в себя примерно атомов, то есть во многих отношениях это довольно большая частица.

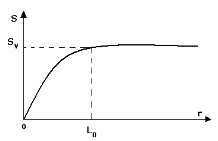
Рисунок 2.1 – Типичная кривая зависимости параметра (S) физического свойства от размера частиц, S_v - объемное значение параметра. L₀ - максимальный наноразмер

На рис. 2.2 приведена электронограмма косой текстуры поликристалла слоистого силиката. Толщина чешуек не превышала 60 нм, но на картине дифракции видно, что рефлексы резкие.

Рисунок 2.2 – Электронограмма косой текстуры флогопита. Толщина чешуек не превышает 60 нм

Расчет электронограммы показал, что структура исследуемого объекта полностью соответствует объемной фазе. Дифракция электронов на монокристалле слюды толщиной не более 30 нм показывает, что при этих толщинах кристалл представляет собой объемную фазу (рис. 2.3).

Рисунок 2.3 – Электронограмма монокристалла слюды. Толщина кристаллов не превышает 30 нм

Можно привести и другие аргументы, подтверждающие условность и несостоятельность единого для всех веществ критерия геометрических размеров веществ наносистем. Например, у многих органических, в том числе и биологических молекул, обнаружено проявление наносвойств, хотя сами эти молекулы могут превышать по своим размерам 100 нм. В то же время, очевидно, что вещество с наноразмерами имеет свойства, отличные от свойств объемного вещества, из которого оно было получено при диспергировании или в которое наночастица перейдет при дальнейшем своем росте. Следовательно, можно говорить о наносостоянии как о новой форме веществ, а переход от нановеществ к объемной фазе и наоборот следует рассматривать как своеобразный фазовый переход. Численным параметром этого перехода является геометрический размер.

Кривая, проведенная на рис. 2.1, может быть описана следующей формулой:

(2.1)

Действительно, при r в интервале 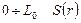монотонно возрастает. При r=0 S(r)=0, при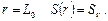

Если , то 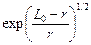становится комплексной величиной и условие (2.1) примет вид:

(2.2)

но модуль функции вида f(x)=exp i равен единице. Следовательно, при

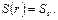
Расчет геометрического критерия наноразмерности, по нашему мнению, должен учитывать, во-первых, свойства вещества, то есть для различных веществ L₀ будет иметь различные значения. Во-вторых, расчет L₀ должен обосновываться представлениями в рамках современной физической парадигмы. В-третьих, при расчете L₀ необходимо использовать уже имеющиеся в арсенале физики табулированные значения физических характеристик вещества. В-четвертых, формула расчета L₀ должна быть достаточно простой, а рассчитываемые значения L₀ должны коррелировать с экспериментальными результатами.

При этом следует иметь в виду, что L₀ не является резкой границей между нано- и объемным состояниями. Следовательно, в качестве исходной табличной величины можно взять такую характеристику вещества, которая разграничивала бы механизмы протекания физических процессов без существенного изменения кристаллохимической структуры. Переходы такого типа можно условно назвать фазовыми переходами третьего рода.

Теоретической основой расчета геометрического размера наночастицы нами была взята квантовая теория, а в качестве основного параметра для расчета критерия наноразмерности использована дебаевская температура, которая табулирована для многих веществ. Если значения дебаевской температуры отсутствует, то она с достаточной точностью, может быть рассчитана по такому параметру, как скорость распространения звука. При этом можно учесть и анизотропию этой скорости, что дает возможность учитывать анизотропию наноразмерности, если она имеется.

Работы Дебая, как и других исследователей, показали, что идеи атомизма и дискретности блестяще согласуются с его выводами, а введенная им температура стала важной характеристикой вещества.

Среди наиболее эффективных приложений температуры Дебая можно назвать теорию теплоемкости при постоянной объеме , которая, как известно, имеет постоянное значение при охлаждении до некоторой критической для каждого вещества температуре, а затем начинает монотонно уменьшаться и становится равной нулю при экстраполированию кривой 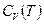в точку Т=ОК. Теплоемкость при постоянном объеме на основе Дебаевских приближений [8] имеет вид:

(2.3)

где, U – внутренняя энергия, 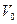– скорость распространения нормальных колебаний, 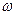– частота, причем

(2.4)

где 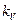- волновой вектор; 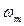- соответствует состоянию, когда полное число нормальных колебательных мод равно 3n, где n – плотность атомов.

Обозначив 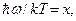выражение (2.4) можно записать как:

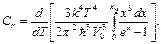(2.5)

Верхний предел x_m равен

(2.6)

Это условие и определяет температуру Дебая , которая, как следует из сказанного, зависит от состава и структуры вещества.

При низких температурах, когда величина х достаточно велика, интеграл в выражении (2.5) имеет значение:

(2.7)

В этом случае 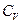(формулы (2.3) и (2.4)) примет вид:

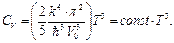(2.8)

Это выражение известно как закон Дебая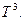

Так как максимальное значение волнового вектора связано с числом атомов (N) условием

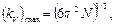(2.9)

то есть

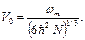(2.10)

Тогда выражение (2.8) с учетом (2.9) и (2.10) примет вид:

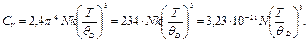(2.11)

Если температура вещества высокая, т.е. отношение имеет маленькое значение, то разложив 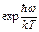в ряд и ограничиваясь вторым членом ряда, получим

(2.12)

то есть

(2.13)

Как следует из условия (2.13), удельная теплоемкость в этом случае становится величиной, не зависящей от температуры (закон Дюлонга и Пти).

При низких температурах в кристалле возбуждаются длинные акустические волны, характерные для непрерывной макроскопической среды. Эти колебания рассматриваются в классическом приближении. Из соотношений (2.8) и (2.11) следует, что доля таких колебаний пропорциональна .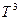

Дата добавления: 2014-12-27