Силикатные наноразмерные частицы

Низкоразмерные частицы природных силикатов широко используются в качестве функциональных модификаторов композиционных материалов на основе матриц [19, 165-170]. При введении допинговых добавок наносиликатов наблюдается синергический эффект повышения триботехнических, адгезионных и физико-механических характеристик [19, 170]. Характеристики полимерных нанокомпозитов в значительной мере определяются размером и технологией получения частиц силикатного модификатора. Установлено, что термообработка порошкообразного полуфабриката в заданном интервале обеспечивает формирование наночастиц с высокой активностью [19, 170]. При выборе технологических параметров термообработки с целью получения активных низкоразмерных частиц необходимо учитывать особенности кристаллохимического строения природных силикатов.

К числу распространенных сисликатных модификаторов полимерных матриц относятся слюды, типичный неорганический природный полимер. Специфическое строение этого слоистого минерала обусловливает различные механизмы и кинетику протекания физико-химических процессов в диапазоне температур 100-1500 ^оС, приводящих к разрушению исходных структур и образованию низкоразмерных частиц [19].

В работах [170, 176] была предложена методика расчета геометрического критерия размеров наночастиц 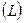. Если размер частицы l удовлетворяет условию 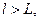то эта частица имеет физические свойства, совпадающие со свойствами аналогичного ей вещества в большом объеме. Если 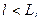свойства частиц начинают зависеть от ее размера, и она может быть названа наночастицей. Наносвойства частиц будут выражены тем сильнее, чем сильнее неравенство

Расчет величины 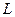, при которой происходят изменения механизмов протекания физических процессов в низкоразмерных частицах, основан на тех же принципах, что и расчет температуры Дебая 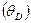. Если температура вещества 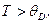то для описания происходящих в нем процессов могут быть использованы методы классической физики. В частности 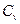таких веществ становится величиной постоянной и подчиняется закону Дюлонга и Пти. Если 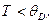то 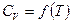и монотонно уменьшается с уменьшением температуры. Для объяснения этой зависимости необходимо привлекать квантово – механические представления. Температурная граница 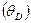между зависимостями и 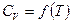и есть температура Дебая. При 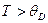распределение фононов в веществе подчиняется классической статистике, при 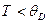– квантовой. Частотная граница собственных колебаний фононов, равная

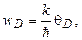(1.48)

где 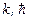– постоянные Больцмана и Планка соответственно) называется дебаевской частотой, причем, как следует из [19]

(1.49)

где – средняя скорость звука в веществе, 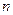– концентрация атомов.

Геометрический параметр наноразмерности имеет вид:

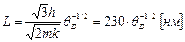, (1.50)

где L и является геометрическим критерием наноразмерности. Расчет величины L с учетом выражений (1.48-1.50) можно выполнить и по формуле:

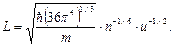(1.51)

После подстановки констант в формулу (1.51) получим:

(1.52)

Если N – число атомов в ячейке кристалла, а V – ее объем в 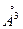, то условие (1.52) примет вид:

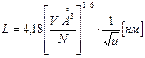. (1.53)

Средняя скорость звука (u) слюд в зависимости от их состава и дефектности лежит в интервале 2000 м/с – 3500 м/с, причем нижняя граница больше соответствует направлению распространения звука перпендикулярному, а верхняя – параллельному плоскости спайности [175, 176]. Этим значениям u соответствует интервал значений L, равный: 12 нмÐ 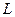Ð16 нм.

Обычные представления о процессах, происходящих в кристаллах при нагревании, сводятся к описанию колебаний атомов вокруг положения равновесия в кристаллической решетке. При этом увеличивается энергия колебаний атома, и, когда она становится больше энергии связи, атом начинает мигрировать по пространству кристалла. Перемещение атомов может происходить двояко: либо в виде непосредственного перехода атома в новое положение, либо как сложный переход, когда атом в течение некоторого времени находится вне обычных узлов решетки, то есть движется в «пространстве междуузлий» до тех пор, пока не займет новое устойчивое положение [173]. Следовательно, тепловое движение атомов в кристалле (и в любом твердом теле) слагается из:

- колебаний атомов вокруг из равновесных позиций;

- диссоциации связанных взаимодействием атомов;

- перемещения диссоциированных атомов путем элементарных перемещений по междуузлиям;

- ассоциации диссоциированных атомов;

- перемещения вакансий.

Процессы, происходящие в слюдах при их нагревании, рассмотрим на примере слюд. Наиболее типичными представителями слюд являются мусковиты и флогопиты. Атомная структура слюды-мусковита представлена на рис. 1.72, на котором изображены два последовательных слюдяных блока, спроецированные на координатные плоскости xz (рис. 1.72 а) и yz (рис. 1.72 б). Средние значения параметров ячейки приведенного на рис. 1.72 (а, б) мусковита равны: а=5,18 Ǻ, в=9,02 Ǻ, с=10,02Ǻ. .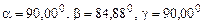

Как видно из рис. 1.72 а, б, атомы в мусковите расположены слоями и связаны между собой в основном блоке (между слоями калия) валентными связями высокой прочности.

Обычно структуры неорганических кристаллов сложного состава изображают так называемыми полиэдрическими моделями, которые строят исходя из следующих соображений. В минералах и других кристаллах все атомы по сродству к электрону разделяются на два типа: анионы и катионы. Центры анионов соединяются отрезками прямых, что приводит к выделению структурных полиэдров из анионов.

В центрах этих полиэдров находятся катионы. Именно такая полиэдрическая модель мусковита изображена на рис. 1.73. В вершинах тетраэдров находятся атомы кислорода, а в их центрах – атомы Si и Al. Вершинами октаэдров являются атомы О и группы (ОН), а сами они заполнены атомами Al.

Природные слюды – это кристаллы с различными составами, но их структуру можно описать в рамках единого подхода на основании полиэдрической модели.

Кристаллическая структура слюд сформирована из двух плотно упакованных слоев кислорода, часть атомов которого замещается группой ОН (или F). В октаэдрических пустотах этой сетки размещаются атомы двух или трехвалентных металлов (атомы А на рис. 1.73).

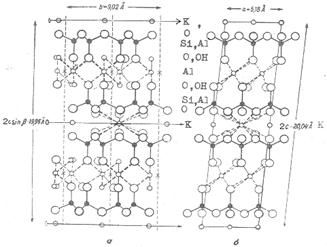
Рисунок 1.72 – Проекции атомной структуры мусковита на координационные плоскости yz (a) и xz (б)

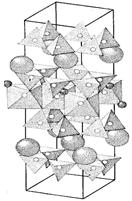
Рисунок 1.72 – Полиэдрическая модель структуры мусковита (с выделенной элементарной ячейкой).

Крупные шары между присоединяющимися по обеим сторонам к октаэдрическому слою тетраэдрическим слоями – ионы К⁺ [174]

Если атом А является трехвалентным, то в соответствии с принципом электростатической нейтральности Л. Полинга ими заполняется только 2/3 общего числа октаэдров и такие слюды называются диоктаэдрическими. В триоктаэдрических слюдах в октаэдрической сетке (ОС на рис. 1.73) заполнены все октаэдрические пустоты (три из трех). К октаэдрической сетке по обеим ее сторонам примыкают по одному слою кислорода, часть атомов которого отсутствует, то есть в этой сетке возникают «лунки», образованные основаниями кислородных тетраэдров. Внутренняя вершина тетраэдра является одновременно вершиной октаэдра.

В тетраэдрических пустотах внешних сеток слюдяного блока размещаются атомы Si, часть из которых замещены атомами Al (или частично других элементов – T). В слюдяном блоке возникает избыточный отрицательный заряд, который компенсируется межслоевым катионом (атомы М на рис. 1.73).

Слюды – минералы с большой склонностью к изоморфизму. Их обобщенная кристаллохимическая формула имеет вид:

,

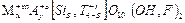где М, А, Т – межслоевой, октаэдрический и тетраэдрический катионы (в соответствии с рис. 1.73). Верхний индекс – валентность, нижний – число атомов, причем: 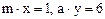, величина 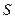зависит от 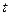. В качестве М выступают ионы ; в качестве А – ; в качестве Т - . Возможны вхождения в слюды комбинаций этих и некоторых других атомов, но во всех случаях должен выполняться принцип электростатической нейтральности. Межатомные связи в пределах слюдяного блока носят явно выраженный валентный характер, тогда как сами блоки связаны слабыми ван-дер-ваальсовыми силами, в основе которых лежит взаимодействие межслоевых катионов с гидроксильным диполем внутреннего октаэдрического слоя. Группа является только вершиной октаэдра и расположена под лункой тетраэдрической сетки, в которой размещается межслоевой катион. Эти структурные особенности слюд объясняют их весьма совершенную спайность и пластинчатый габитус, характерные как для больших кристаллов, так и для нанокристаллов.

В природе встречаются не только трехслойные силикаты (слюды) с последовательностью слоев в блоке … ТС-ОС-ТС…, но и двухслойные с последовательностью … ТС-ОС…. Возможны случаи вхождения в межслоевой промежуток слоистого силиката не только межслоевого катиона, но и группы атомов, формирующих свой структурный полиэдр. Все это объясняет наличие достаточно большого числа разновидностей слоистых силикатов.

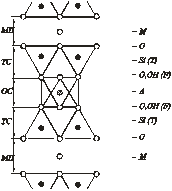
Рисунок 1.73 – Схема атомной структуры слюдяного слоя: О – атомы кислорода; Si – атомы кремния (T – тетраэдрический, А – октаэдрический, М –межслоевые катионы); ОН – гидроксил; F – атом фтора; ОС – октаэдрическая сетка; ТС – тетраэдрическая сетка; МП – межслоевой промежуток

В качестве примера укажем лишь на некоторые слоистые минералы [19, 175], нашедшие применение в различных областях, в т.ч. в материаловедении:

двухслойные минералы:

Тальк - ;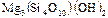

Пирофиллит - ;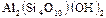

Каолинит (диккит, накрит) - .

трехслойные минералы:

Мусковит - ;

Флогопит - ;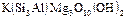

Биотит - ;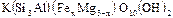

Парагонит - ;

Лепидолит - ;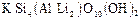

Циннвальдит - ;

Маргарит - ;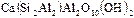

Зейбертит - ;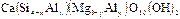

Монтмориллонит - .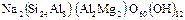

четырехслойные минералы:

Вермикулиты - .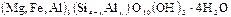

Атомы в кристалле могут находиться в различных кристаллоэнергетических позициях, тогда смещения некоторых атомов из равновесных положений могут наступать при различных температурах. Это обстоятельство очень хорошо объясняет возможность выхода гидроксилов из октаэдрического слоя элементарного блока слюд до разрушения кристалла. Выход гидроксилов облегчается еще и тем, что для него есть довольно большой канал, по которому это группа может мигрировать в межслоевой промежуток. Наличие гидроксила в слюдах определяет механизм термического разрушения их кристаллов.

Изменения в октаэдрическом слое слюд при определенных температурах (как показывают эксперименты, для мусковита при температурах 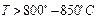, для флогопита при 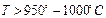) достигают таких величин, что никакие развороты тетраэдров не могут привести к соответствию этих двух слоев [174]. Слюдяной блок разрушается. Качественно механизм термических изменений при высоких температурах можно описать следующим образом.

При нагревании группа 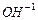, как и отдельные атомы, начинает увеличивать энергию своих тепловых колебаний. Если у отдельных атомов эти колебания сводятся лишь к увеличению их энергии, то для группы 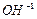необходимо учитывать взаимосмещения протона и 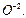Надо также учитывать и тот факт, что в октаэдрах находится не одна, а две группы 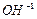, причем октаэдры могут встречаться в двух типах. У одних из этих структурных полиэдров гидроксилы находятся на ребре октаэдра (цис-октаэдры), у других они связаны телесной диагональю (транс-октаэдры) [174].

При повышении температуры вследствие увеличения амплитуды (и частоты) валентных колебаний в группе 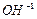существенно возрастает вероятность взаимодействия протона с соседней группой 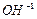. При этом, естественно, образуется молекула 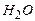, которая, в силу своей электонейтральности, слабо связана с остальными элементами структуры и начинает мигрировать через канал тетраэдрического слоя в сторону межслоевого промежутка. Координация октаэдрического алюминия становится равной пяти. Это вызывает изменение координат оставшихся в октаэдрическом слое атомов кислорода, причем все эти атомы, кроме заменившего две гидроксильные группы, являются внутренними вершинами тетраэдров внешнего полиэдрического слоя элементарного блока. Для выполнения структурного соответствия между октаэдрической и тетраэдрической сетками тетраэдры должны развернуться вокруг, практически произвольных (не параллельных, и не перпендикулярных плоскости спайности) осей. В кристаллах слюды возникают области с сильными механическими напряжениями. Кристалл растрескивается. В областях растрескивания возникают новые поверхности, что облегчает выход других атомов из кристаллов.

Выход группы 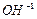из октаэдрического слоя может быть зафиксирован дифракционными методами. Так как указанные изменения структуры нагляднее проявляются на проекциях 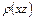или 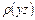, то нами исследовались рефлексы серии 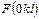, что потребовало трукальной обработки образцов с определением ориентации для получения поверхностей с требуемыми индексами граней. Наряду с рентгенодифрактометрическим методом «на отражение» использовали метод «на просвет», а также был выполнен и термоэлектронографический анализ влияния нагревания на структуру слюд [174]. Знаки 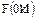определены по идеальной модели мусковита. Нормировка осуществлена по рефлексу 00.10. Политипная модификация 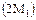определялась по классической методике, описанной в работе [175].

Точечная группа слюд характеризуется наличием центра симметрии. Поэтому структурные амплитуды – действительные, а не комплексные величины. В некоторых случаях возможны такие размещения атомов, что центральная симметрия несколько нарушается. Тогда в структурной амплитуде, наряду с действительной частью 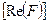, появляется и мнимая составляющая 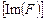. Однако последняя настолько мала, что отношение 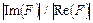практически не превышает погрешности эксперимента, которая при определении 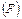в нашем случае составляла примерно 3 %

В общем случае формула для расчета распределения электронной плотности для центросимметричных кристаллов имеет вид:

. (1.54)

При расчете проекций электронной плотности на координатную плоскость необходимо брать рефлексы с индексами :

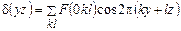. (1.55)

В табл. 1.17 представлены экспериментальные значения труктурных амплитуд 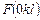кристалла мусковита при температуре 20 ^оС и прогретого при 850 ^оС в течение 150 часов.

Нагревание проводили со скоростью , так как при более высокой скорости нагрева в образце возникают трещины, что делает невозможным качественное выполнение структурных исследований.

Таблица 1.17

Дата добавления: 2014-12-27