Связь фононных характеристик с наноразмерностью

При рассмотрении атомных процессов в твердых телах часто используют классические представления (примерами может служить элементарный акт диффузии; расчет теплоемкости при температурах, близких к нормальным, расчет механических параметров, например, коэффициента упругости и др.). Широкую область применения классический подход (описание с помощью классической, а не квантовой механики) имеет при исследовании теплового движения атомов (ионов), то есть их «колебательный контур» вокруг положений равновесия. Так как это утверждение носит качественный характер, то следует, хотя бы кратко, остановиться на применимости квантового подхода к описанию этих явлений, что позволяет ввести важное для всей физики твердого тела понятие – дебаевская температура.

Рассмотрим простейшую модель теплового движения атомов в веществе, считая, что твердое тело – это система из осцилляторов, колеблющихся с одинаковой частотой 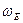. Заметим, что число осцилляторов должно совпадать с числом колебательных степеней свободы, равным 3N, для кристалла с атомами одного типа. N – это число атомов в кристалле. Такую модель для описания тепловых свойств твердых тел использовал А. Эйнштейн, первым применивший законы квантовой механики к вычислению теплоемкости при низких температурах. В квантовой физике до настоящего времени иногда используется понятие «действие» с размерностью (отсюда h – квант действия). Для осциллятора действие где Е – энергия осциллятора, а - частота осциллятора, который считается гармоническим, причем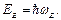

Характерное значение действия осциллятора, принимающего участие в тепловом движении, согласно классической статистике равно:

(2.14)

где k – постоянная Больцмана, Т – абсолютная температура.

Так как среднее значение энергии это

(2.15)

величину 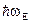(квант колебательной энергии) называют энергией или температурой Эйнштейна которая измеряется по энергетической шкале.

Если , характерное действие значительно больше постоянной Планка 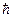, а, значит, колебательное движение атомов действительно можно описывать, пользуясь классической, а не квантовой механикой. При 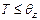классический подход не применим. Однако, спектр частот осцилляторов не ограничивается одной частотой, а занимает целую полосу (одно из наиболее важных положений модели твердого тела предложенной Дебаем) от нуля до характерного для каждого кристалла значения (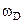). Температура Дебая определяется энергией колебательного кванта с максимальной частотой, то есть частота колебательного кванта w, называемого фононом, должна удовлетворять условию (2.16):

(2.16)

и при любой (даже достаточно низкой) температуре найдутся осцилляторы, движение которых можно описывать классическими формулами. Но только при 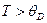все осцилляторы допускают классическое описание. Таким образом, температура Дебая разграничивает шкалу температур: выше температуры Дебая допустимо классическое описание колебательного движения атомов твердого тела, ниже – необходимо квантовое приближение. Подчеркнем, что речь идет только о колебаниях атомов или ионов. Для описания движения электронов практически всегда необходимо исходить из квантовых законов. Температуры Дебая разных веществ приведены во всех справочниках по физике твердого тела.

П. Дебай, описывая фононы, распределил их не по отдельным атомам или молекулам, а по нормальным колебаниям всего кристалла в соответствии с температурной зависимостью для планковского резонанса. Само твердое тело рассматривалось им как классический континуум.

Эффекты размерного ограничения на поведения носителей зарядов достаточно подробно рассматривалась в ряде работ (см. например [9-12]). В частности было установлено, что эффекты размерного квантования появляются на кривых зависимостей критической температуры от толщины пленки Этот параметр влияет на спектр фононов. Обусловлено это прежде всего тем, что объемные фононы заменяются спектром размерно-ограниченных фононов тонких пленок, для которых величина d не превышает значений 2 нм, а дебаевская температура составляет 100 К. Для этой температуры верхний размер наносвойств составляет, согласно модели, приведенной в работе [15] и равен 23 нм. Результаты многих работ [2-6, 15, 16] не противоречат этому, так как ее авторы изучали сверхпроводящие свойства на предельно малых толщинах пленок . Только в этом случае можно увидеть эффекты размерно-ограниченного квантования, которое проявится именно для электронов [9-12]. Следовательно, в качестве разграничения объемных и наноразмерных структур требуется применять такие размеры, при которых исчезает влияние размерно-ограниченного квантования именно для электронов.

Влияние размерного ограничения «конфайнмента» для фононов в наноструктурах проявляется, в конечном итоге, в размерном ограничении движения электронов, которое обуславливает не только перенос заряда, но и перенос механических возбуждений. Для фононов размерные ограничения проявляются в том, что фазовое пространство становится ограниченным и представление фонона в виде плоской волны перестает быть правомерным. Причем, эти ограничения касаются как оптических, так и акустических фононов. Авторы работы [4] для кристаллов выделяют две модели: континуальную и микроскопическую. Граница применимостей этих моделей подразумевается нерезкой, но, к сожалению, численные параметры разделения вещества на объемное и наноразмерное не обозначены.

Температура Дебая была введена для описания фононов – этих квантов поля механического возбуждения. Фононные явления неизбежно испытывают размерные ограничения и их поведение в наночастице в значительной мере подобно поведению электрона в потенциальной яме на наш взгляд, совершенно логично использовать для оценки граничных размеров наночастиц теорию, разработанную для фононов, то есть взять из нее такую характеристику вещества, как температура Дебая .

Температура Дебая определяет как дебаевскую энергию 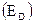так и дебаевский импульс ():

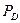(2.17)

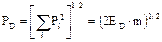(2.18)

где i – индекс координатной оси, т.е. i=x, y, z.

Так как механическое смещение ядра приводит к возбуждению электронов, переводя их на уровень, превышающий основной на энергию фонона, то в формуле (2.18) следует брать m равной массе электрона. Дебаевский импульс есть граничное значение для использования различных приближений (классического и квантового). При переходе к кристаллам малых размеров характер распределения фононов отличается от процесса в объемном кристалле. Очевидно, что фононы с длиной волны 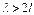(l – размер частицы), существовать не могут. Применив соотношение неопределенностей при учете получим значение размера частицы при котором происходит изменение свойств вещества, то есть частица приобретает свойства, обусловленные размерными факторами. Следовательно,

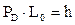(2.19)

и подставив в уравнение (36) значение дебаевского импульса с учетом (2.18) вдоль одной из координационных осей получим:

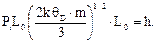(2.20)

Отсюда

(2.21)

Так как

то Следовательно, предельное значение размера наночастицы равно

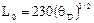[нм]. (2.22)

Температура Дебая – это довольно условная характеристика вещества, так как ее определение основано на ряде приближений. Однако этот параметр вошел в справочники и широко используется в физике конденсированных состояний. При анализе этой величины обращает на себя внимание факт расхождений значений 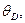зачастую превышающий 10 %, что обусловлено различными методами ее определения.

Значение дебаевской температуры связано с величиной 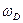(см. (2.16)) условием

(2.23)

где, U – скорость звука в веществе, n – число атомов в единице объема, 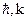– постоянные Планка и Больцмана соответственно.

Как правило, величину рассчитывают по известным формулам, исходя из экспериментальной скорости звука, а затем корректируют по кривой экспериментальной зависимости при низких температурах.

В работе [7] говорится, что на кривой надо брать область температур 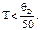Так как распространение фононов в веществе определяется механическим возбуждением, имеющим анизотропный характер, то параметр (см. (2.21) – также анизотропная величина, то есть для разных направлений в кристалле предельные размеры наночастиц могут отличаться. Однако связана с теплоемкостью 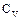, которая является скалярной величиной. Следовательно, определяет также не строгую, а некую условную величину для определения размеров наночастиц. Чем сильнее неравенство (r – размер частиц), тем сильнее проявляются размерные эффекты, то есть тем сильнее свойства частицы отличаются от объемных.

Характеристическая температура – величина скалярная, однако в формулу ее расчета (см. (2.23)) входит скорость распространения нормальных колебаний, то есть скорость звука . Эта характеристика зависит от кристаллохимической структуры вещества [6] следовательно, - величина анизотропная. Отсюда вытекает очень важный, на наш взгляд вывод. Размерная граница между наносостоянием и объемной фазой – этот параметр, в общем случае, анизотропный и для одного и того же вещества для различных направлений может быть постоянной величиной [13, 14], то есть может быть описана образной фигурой. Для кубических кристаллов – это сфера. Для кристаллов средних сингонией (три-, тэтра- и гексагональная) эта образная фигура – эллипсоид вращения (вытянутый или сжатый). В кристаллах низших сингоний (ромбическая, моноклинная, триклинная) характеристической фигурой размерной границы между наночастицей и объемной фазой является трехосной эллипсоид. Очевидно, что анизотропия может встречаться и в наночастицах, полученных из некристаллического (например, полимерного, биологического и др.) вещества. Кроме того, возможна ситуация, когда частица в одном направлении имеет минимальное значение толщины, например, , а в перпендикулярных ему 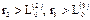. В этом случае следует говорить об одномерной наночастице, которая имеет форму чешуйки. Если 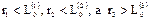, то это двумерная наночастица (нанонить или вискер). Если 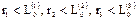, то такая частица – это трехмерная наночастица (или просто наночастица) [14].

Дата добавления: 2014-12-27