Модельные представления о механизме модифицирования полимерных матриц нанокомпозиционными частицами

Как ранее отмечалось, нанокомпозиционные машиностроительные материалы на основе полимерных матриц находят все большее применение при создании герметизирующих устройств, узлов трения машин, механизмов и технологического оборудования, функциональных покрытий. Марочный ассортимент низкоразмерных модификаторов непрерывно расширяется и включает металлические, силикатные, углеродные компоненты в виде простых веществ и соединений типа нитридов, карбидов, солей и др. [16-27, 65-67]. Это требует разработки методологии оптимального выбора модификаторов, обеспечивающих заданный уровень служебных характеристик композиционных материалов.

В настоящем разделе рассмотрены физические аспекты модифицирующего действия наноразмерных частиц наполнителя в модельных системах на основе полимеров.

В модельных композиционных системах, которые состоят из связующего и наполнителя, можно выделить три характерных типа веществ (рис. 2.39): вещество частицы (Ч), связующее (С) и прилегающая к частице часть связующего (граничный слой, П).

Рисунок 2.39 – Составные части модельного композита: частицы наполнителя (Ч), связующее (С), граничный слой (П)

Таким образом, экспериментальные данные, полученные из литературных источников и проведенных исследований, свидетельствуют о наличии характерного энергетического состояния поверхностных слоев компонентов трибосистемы, которое вносит существенный вклад в механизм ингибирующего действия функциональных наноматериалов.

Рассмотрим простейший случай, когда наночастицы и модифицированные ими области имеют сферические формы. Пусть объем системы равен u, число наночастиц равно N, радиус частицы r_j, толщина модифицированного приповерхностного поля h_j.

Следовательно, объем частицы равен 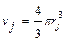, объем модифицированной области W_j:

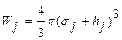. (2.155)

Если N – число частиц, V_j – объем j -той частицы, то величина С_v

(2.156)

определяет относительный объем, занятый наночастицами, или коэффициент заполнения (коэффициент упаковки). Отношение

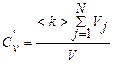(2.157)

представляет собой относительный модифицированный объем, <k> - коэффициент перекрытия участков, модифицированных частицей наполнителя.

Из экспериментов известно, что даже при небольшой концентрации наноразмерных частиц модификатора (до 0,1 мас.%) свойства композита на основе полимера могут существенно изменяться. В частности, для деталей изготовленных из модифицированных термопластов, износостойкость и прочностные характеристики могут увеличиваться на 20–30 % [16, 22, 23, 37]. Для объяснения этого экспериментально зафиксированного факта можно использовать следующую модель.

Пусть массовая концентрация частиц наполнителя С_m, масса и плотность наполнителя m_f и r_f соответственно, m_в, r_в – то же для связующего. Тогда:

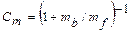. (2.158)

Отсюда, объемная концентрация наполнителя (2.156) равна:

. (2.159)

Если объем (и радиусы) частиц модификатора одинаков, то:

. (2.160)

Пусть толщина модифицированного слоя равна h, тогда для достижения полного модифицирования необходимо выполнение условия:

. (2.161)

где К – коэффициент, учитывающий перекрывание и компактность модифицирующих областей.

Из условий (2.160) и (2.161) следует:

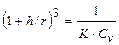. (2.162)

Так как m_в>>m_f, то условие (2.159) можно представить в виде:

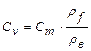. (2.163)

Тогда выражение (2.162) примет вид:

. (2.164)

Для предельного случая, когда частицы располагаются в точках, соответствующих плотнейшей упаковке шаров с радиусом (r+h), и перекрывание отсутствует, К =0,74. При r_f/r_в =4 (достаточно типичный случай) и С_в = 0,1 % получим:

h»15 r. (2.165)

Естественно, применение предложенной модели имеет ограничения, потому что, во-первых, надо доказать, что условие (2.165) выполнимо, а, во-вторых, необходимо учитывать, что при создании композита трудно достичь равномерного распределения модифицирующих частиц по объему связующего. Действительно, в работе [72] показано, что в соответствии с эргодической теоремой в каждой точке вещества композита при его перемешивании происходят флуктуационные изменения плотности, то есть возникают дивергентные потоки, что обуславливает возникновение и исчезновение кластерных структур. При этом возможно не только образование, но и разрушение кластеров (рис. 2.40).

Известно, что многие низкоразмерные частицы обладают собственным нескомпенсированным зарядом с большим временем релаксации [23, 37, 66]. Если модифицированный объем в композите рассматривать как молекулярный кластер, то его формирование вокруг заряженной частицы модификатора можно описать следующим образом. Вследствие того, что увеличение размеров кластеров происходит в результате взаимодействия поляризованных молекул среды, то из теоретического анализа процессов создания композита в рамках различных приближений всегда следует вывод, что процесс образования кластеров в композиционных полимерных системах неизбежен. Для моделирования этого явления возможно использование представлений, изложенных в [73, 74].

а б в

Рисунок 2.40 – Переход частицы от одного 10-ти частичного кластера к другому: а – исходное положение, б – движение частицы через потенциальный барьер, в – укрупнение и уменьшение кластеров

допинговых Рассмотренная модель с учетом 2.165 и [73-79], позволяет понять модифицирующее действие, то есть малых массовых концентраций наноразмерных частиц. Однако, для более строгого аргументирования адекватности этой модели реальным процессам необходимо обосновать возможность возникновения зарядов на поверхности нанокристаллических частиц [80-88].

Для экспериментальной проверки полученных модельных представлений о механизме реализации модифицирующего действия наноразмерных частиц в полимерных матрицах были получены композиты с допинговыми добавками ультрадисперсных частиц углерода детонационного синтеза (УДАГ).

В качестве объекта исследования был использован полиэтилен низкого давления (ПЭНД) марки 227-03 (ГОСТ 16338-85) и полиэтилен высокого давления (ПЭВД) марки 16207-029 (ГОСТ 16337-85). Полимеры модифицировали ультрадисперсными частицами углерода, полученными методом детонационного синтеза (шихта). Удельная поверхность частиц наполнителя составляла 300±30 м²/г. Размеры единичных частиц наполнителя составляла 3-8 нм, а устойчивых агрегатов – 20-30 нм. Композиции готовили методом механического смешивания порошков исходных полиолефинов с наполнителем. Образцы для физико-механических испытаний получали методом литья под давлением [80].

Для определения структурных изменений модифицированных ПЭНД и ПЭВД анализировали рентгенограммы, полученные на рентгеновском дифрактометре ДРОН-2,0 при фильтрованном CuK_а излучении.

Средний размер областей когерентного рассеяния (L) рассчитывали по формуле Шеррера:

,

где 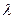- длина рентгеновского излучения (1,54 Ǻ), - полуширина и угловое положение максимума соответственно [84].

Для более детального рассмотрения структурных изменений в ПЭ при введении ультрадисперсных кластеров наполнителя строились корреляционные функции W(r), связанные с функциями радиального распределения атомной плотности (ФРРАП) 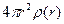, методика построения которых описана в работах [85-87].

На рентгенограммах ПЭНД и ПЭВД, модифицированных частицами шихты, в области углов дифракции 2Q=15^о-25^о наблюдается гало с наложенными на него достаточно выраженными максимумами в области углов 2Q=37^о-46° имеется второе более размытое гало (рис. 2.41). Анализ рентгенограмм свидетельствует о том, что существенного изменения содержания кристаллической фазы в композитах не происходит.

В табл. 2.7 приведены экспериментальные значения размеров областей когерентного рассеяния (L Ǻ, см) в зависимости от массовой концентрации (С, мас.%) шихты. Видно, что, во-первых, изменения L для различных образцов в ряде случаев существенно превышают погрешности эксперимента, а, во-вторых, L не изменяются монотонно с ростом С, мас.%. Действительно, для ПЭНД

%

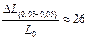При экспериментальной погрешности 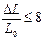%. В то же время

, но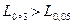

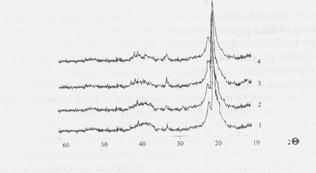
Рисунок 2.41 – Рентгенограммы полиэтиена высокого давления, модифицированного УДА с различной массовой концентрацией (С, мас.%): 1 – исходный, 2 – 0,01 мас.%, 3 – 0,01 мас.%,
4 – 1,0 мас.%

Таблица 2.7

Зависимость размеров областей когерентного рассеяния (L Ǻ) от массовой концентрации (С, мас.%) ультрадисперсного углерода (шихты)

С, мас.%		0,01	0,03	0,05	0,1	0,3	0,5	1,0
ПЭВД (L Ǻ)
ПЭНД (L Ǻ)

Введение добавок шихты даже при небольших концентрациях приводит к существенным изменениям структурных параметров полимера. Отметим, что изменение корреляционных функций наблюдается не только при введении малых количеств шихты, но и мелкодисперсных частиц других веществ (рис. 2.41).

Из таблицы видно, что при введении даже малого количества модификатора наблюдается увеличение ОКЧ до 1,13 для ПЭВД при С=0,03 мас.% и до 1,27 для ПЭНД при С=0,01 мас.%. Это может быть связано с изменением размеров областей когерентного рассеяния в аморфной матрице полимера. Введение модификатора вызывает изменения радиусы первых координационных сфер, которые соответствуют связи С-С [90].

Рисунок 2.41 – Рентгенограммы полиэтилена низкого давления, модифицированного УДА с различной массовой концентрацией (С, мас.%): 1 – исходный, 2 – 0,01 мас.%, 3 – 0,01 мас.%,
4 – 1,0 мас.%

Дляоценки изменений атомных координаций в полимерной матрице были рассчитаны относительные координационные числа (ОКЧ) [87].

Число атомов в первой координационной сфере исходного полиэтилена принято за 100 % (табл. 2.8).

Методом атомно-силовой микроскопии (АСМ) исследованы ПЭВД и ПЭНД с различной массовой концентрацией наполнителя (рис. 2.42).

Поверхности трения ПЭВД имеет отчетливо ориентированный вдоль направления скольжения рельеф высотной характеристикой R_a=15 нм по полю сканирования 25´25 мкм². характер морфологии поверхности трения свидетельствуют, что для ПЭВД при трении без подвода внешней смазки преобладает деформационная составляющая силы трения.

Введение ультрадисперсных кластеров синтетического углерода приводит к существенным изменениям поверхности трения полимера. Так, при содержании 0,05 % ультрадисперсных кластеров образуются участки с пологим рельефом, однако значения R_a возрастают до 452 нм. Увеличение содержания модификатора в полимере приводит к дальнейшему сглаживанию рельефа и уменьшению размеров «валиков», значения R_a составили 123,8 нм.

Таблица 2.8

Значения радиусов (r, Ǻ) и относительных координационных чисел (ОКЧ) для композитов с различной массовой концентрацией (С, мас.%) наполнителя

С, мас.%		0,01	0,03	0,05	0,1	0,3	0,5	1,0
ПЭВД	ОКЧ	1,00	1,13	1,33	0,78	0,72	1,14	1,03	0,97
r	2,28	2,4	2,3	2,9	1,3	1,3	1,3	1,3
ПЭНД	ОКЧ	1,00	1,27	1,13	1,10	1,10	1,25	0,94	1,14
r	2,3	2,2	2,3	2,5	2,3	2,25	2,25	2,25

а

б

в

г

Рисунок 2.42 – АСМ-снимки поверхности трения ПЭВД, модифицированного УДА: а) ПЭВД, б) ПЭВД+0,05 % шихты, в) ПЭВД+0,5 %, г) ПЭВД+1 % шихты (скорость скольжения 0,5 м/с, контртело сталь 45)

Характер зависимости коэффициента трения от процентного содержания, по-видимому, объясняется структурными изменениями в аморфной части полиэтилена. Так, увеличение модификатора в полимере до 0,03% приводит к возрастанию упорядоченности в аморфной части полиэтилена и как следствие увеличивается напряжение сдвига, что приводит к возрастанию коэффициента трения. При концентрации шихты от 0,05-0,1% дальнейшего упорядочения в аморфной части полимера не наблюдается (табл. 2.8), в результате чего значение напряжения сдвига уменьшается, что приводит к уменьшению значений коэффициента трения.

Таким образом, исходя из результатов проведенных исследований, можно констатировать, что введение даже небольших количеств ультрадисперсных наполнителей приводит к структурным изменениям в аморфной части полиэтилена. Происходит изменение размеров областей когерентного рассеяния, которые связаны с областями локального упорядочения. Очевидно, это приводит к заметным изменениям показателей физико-химических характеристик исследуемых полимеров.

Для ответа на вопрос, почему изменения могут быть вызваны столь малым (до 1,00 мас.%) количеством ультрадисперсного наполнителя (УДН), рассмотрим следующую модель. Пусть концентрация УДН равна С_m объем частицы наполнителя равен V_1H, плотность наполнителя полимера r_н и r_п соответственно. Так как

, (2.198)

где 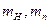- масса наполнителя и полимера соответственно.

Объемная концентрация УДН равна

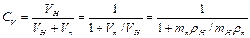, (2.166)

где 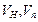- объемы наполнителя и полимера соответственно.

Отсюда связь между 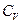и и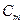меет вид:

, (2.167)

где 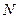- общее число частиц наполнителя, 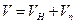- объем вещества, n - концентрация частиц наполнителя.

Объем, приходящийся в среднем на одну частицу (W), равен:

, (2.168)

где С_Н – концентрация наполнителя.

Отсюда следует, что полимер будет полностью модифицирован, если частица УДН оказывает влияние на молекулы связующего в прилегающем к частице слое толщиной L, равном

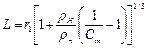, (2.169)

где - размер частицы.

В работах [22, 91, 92] рассмотрены модели частиц УДА, из которых следует, что в этих частицах имеется ядро с алмазной структурой, окруженное аморфизованной углеродной пленкой. Некомпенсированные молекулярные связи на поверхности частицы превращают ее в своеобразный активный центр, действующий на прилегающие к ней слои другого (в нашем случае полимерного) вещества. Аналогичные эффекты были обнаружены для ряда других объектов. В частности, поверхности слоистых силикатов оказывают упорядочивающее влияние на поверхностные водные пленки с толщиной, в сотни раз превышающей размер молекулы воды. Свойства этих пленок (теплопроводность, теплоемкость, сдвиговая упругость и др.) сильно отличаются от аналогичных для объемной воды [93].

Как следует из формул (2.168, 2.169), размер области «влияния» частицы ультрадисперсного наполнителя (УДН) (L) линейно связан с размерами частицы (r ₁) и слабо связан с отношением r_Н/r_n и с концентрацией (С_Н). Выше были приведены экспериментальные данные, показывающие, что изменение в полимере происходят даже в том случае, если концентрация УДН составляет несколько промилле. Добавки такого типа в отличие от других можно назвать допинговыми. Нами в качестве допинговых добавок использованы ультрадисперсные алмазы (УДА). Для допинговых добавок 1/С_m>>1, то есть формула (2.169) может быть представлена в виде

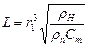. (2.170)

Как показано в работах [12-13] размер частиц УДА, полученных по эксплозивной технологии, составляет примерно 45 Ǻ. Если плотность частиц УДА принять равной плотности объемного алмаза, то выражение (2.170) примет вид:

, (2.171)

то есть даже для концентраций допингового наполнителя равных 1% расстояние, на которое должна подействовать допинговая частица, чтобы вызвать изменения в полимере, не превышает размеров 2-3 слоев полимерных молекул.

Из приведенной модели следует, что при малых концентрациях наполнителя решающую роль играет дисперсность его частиц. Если поверхность частицы УДН оказывает влияние всего на 2¸3 прилегающих к ней молекулярных слоя связующего, то весь его объем может оказаться модифицированным, при этом свойства самих частиц не играют решающей роли. Наши эксперименты показали, что при одинаковой концентрации (не более 5 %) для различных наполнителей свойства композитов совпадали практически в пределах ошибок экспериментов. Изменения отношения r_Н/r_n и концентрации допингового наполнителя на порядок изменяет величину L всего примерно в 2 раза.

Таким образом, на основании выполненных исследований, можно сделать следующие выводы:

1. Предложенная математическая модель модифицирующего действия НРЧ на полимерной матрице позволяет объяснить эти изменения при условии, что поверхность частицы допингового наполнителя оказывает модифицирующее влияние на расстояние L, не превышающее толщину 2¸3 слоев полимерных молекул.

2. Основное влияние на величину L и, следовательно, на изменение свойств полимера оказывает размер частиц допингового наполнителя.

3. Изменение плотности допингового наполнителя (r_Н) и полимера (r_n), а также массовая концентрация наполнителя (С_n) слабо влияют на величину L, так, при изменении r_Н/r_n и С_m на порядок величина L меняется примерно в два раза.

4. В качестве допинговых наполнителей можно использовать не только УДА но и НРЧ других веществ, поверхности частиц которых взаимодействуют с молекулами полимера.

5. При создании полимера с НРЧ особое внимание необходимо обратить на их равномерное распределение в матрице связующего.

Проведенные исследования позволили установить, что на эффективность модифицирующего действия НРЧ оказывают влияние не только параметры структуры и состава, но и формы.

Как ранее отмечалось (гл. 1), наноразмерные характеристики частицы могут проявляться в 3-х, 2-х и одном направлении, что приводит к формальному делению НРЧ на чешуйчатые, вискерные и сферические.

Одномерным нанокомпонентом являются частицы, у которых толщина (ℓ) соответствует критерию наноразмерности, то есть h<L, где , 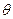– Дебаевская температура. Размеры частицы для направлений, перпендикулярных ℓ, 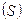, могут иметь значения: . Модифицирующее действие чешуйчатых наночастиц описано, например, в работах [16, 19-21, 23. 25 и др.].

Основными характеристиками модифицирующих чешуйчатых наночастиц являются: h – средняя толщина одномерной наночастицы; S – средняя площадь наночастицы; H – толщина модифицированного слоя матрицы композита приповерхностного по отношению к частице вещества (рис. 2.42); C_V – объемная концентрация модификатора.

Как следует из рис. 2.43, объем композита, модифицированный одной частицей, равен

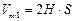. (2.172)

Отсюда степень модифицирования частиц (М), равная отношению суммарного модифицированного объема к общему объему композита, равна

, (2.173)

где n – концентрация частиц модификатора.

Так как

, (2.174)

то максимальная возможная степень модифицирования связующего в нанокомпозите при чешуйчатой форме частиц наполнителя-модификатора равна:

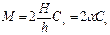, (2.175)

где .

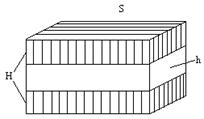
Рисунок 2.43 – К механизму модифицирования одномерным нанокристалом: h – толщина наночастицы, H – толщина модифицированного слоя, S – площадь пластинки

Отсюда следует, что при , при , , т.е. . Следовательно, величина Н определяется не только свойствами наночастицы модификатора, но и величиной 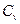. Однако при малых значениях 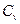основную роль будут играть поверхностные свойства частицы. Из выражения (2.175) следует, что максимальное значение величины 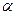при малых значениях 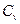и и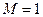меет вид

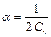. (2.176)

Это значит, что для достижения максимального модифицирующего эффекта при использовании одномерных наночастиц и фиксированном 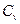необходимо стремиться к уменьшению их толщины. Для слоистых силикатов, в частности, для слюд, h при различных методах измельчения имеет значение h=20Ǻ=2 нм (два слюдяных слоя) [25, 35-37]. Так как значение Н для слюд может иметь значения 100 нм, то

.

Учитывая, что модифицирование полимерного композита не требует изменения всей матрицы, а в ряде случаев достаточно достичь значения М=0,2÷0,3 [25], то объемная концентрация нанонаполнителя в этом случае равна 0,2÷0,4 об.% [19-21, 37].

Наряду с чешуйчатым габитусом частиц наномодификатора в качестве наполнителя полимера можно использовать так называемые «вискеры», то есть двухмерные наночастицы, у которых сечение – круг, со средним радиусом (r), а их средняя длина l>>r. Пусть толщина модифицированного вискерной частицей слоя равна Н (рис. 2.44), тогда модифицированный одной частицей объем 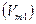равен

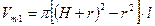, (2.177)

т.е. степень модифицирования (М) равна

, (2.178)

где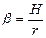

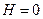При , . Если , то и .

Если наночастица модификатора имеет сферическую форму и ее средний радиус равен r, а средняя толщина модифицированного слоя связующего равна Н, то (рис. 2.45)

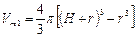. (2.179)

В этом случае степень модифицирования

, (2.180)

где .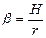

Таким образом, степень модифицирования (М) для наночастиц наполнителя различного габитуса рассчитывается по следующим формулам:

‑ для чешуйчатой частицы:

,

где 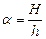(см. рис. 2.43);

‑ для цилиндрической частицы (вискеры):

,

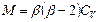где 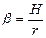(см. рис. 2.44);

‑ для сферических частиц:

,

где (см. рис. 2.45).

Рис. 2.44 – К механизму модифицирующего действия вискерной частицы

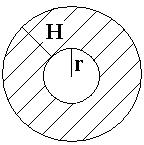
Рисунок 2.45 – К механизму модифицирующего влияния сферической частицы: r – радиус частицы, Н – толщина модифицированного приповерхностного слоя

Рассмотрим случай наполнения полимерной матрицы, когда значение для частиц различных габитусов одинаково, а . Тогда

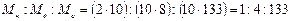. (2.181)

Казалось бы, что согласно этим расчетам при выборе модификатора необходимо отдавать предпочтение сферическим частицам. Однако в соотношениях (2.181) не учтены изменения полей электрически заряженных частиц с различной формой. Если частица не обладает нескомпенсированным зарядом, то ее модифицирующее действие снижается [19-21]. Следовательно, электрический заряд – важнейший компонент модифицирования полимерных матриц.

Если объемная плотность заряда равна 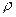, а линейный размер пластины-чешуйки существенно превышает ее толщину, то для слоистых частиц, например, геосиликатов обычно имеет место соотношение. При соотношении напряженность поля в периферии чешуйчатой наночастицы является постоянной величиной, равной

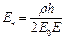. (2.182)

Для вискерной частицы на расстоянии R от оси значение Е определяется из выражения:

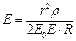. (2.183)

Для сферической частицы, когда R – расстояние точки поля до центра частицы, получим

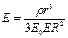. (2.184)

Из сравнения напряженностей поля от заряженных наночастиц с одинаковыми значениями и нм, нм в формулах (2.181-2.184) получим

. (2.185)

Напряженность поля связана с величиной дисперсии углов молекулярных диполей к нормали в точку поверхности частицы, контактирующей с молекулой приповерхностного слоя связующего при прочих равных условиях. Чем выше величина Е, тем больше толщина модифицированного слоя. Следовательно, совместный учет полученных отношений (2.183) и (2.185) показывает, что модифицирующее действие наночастиц чешуйчатых (ч), вискерных (в) и сферических (с) при прочих равных условиях определяется отношением

. (2.186)

Таким образом, при малых концентрациях наномодификатора наиболее перспективным оказывается использование чешуйчатых частиц, к которым относится большая группа слоистых силикатов, широко распространенных в природе. Это обусловило широкое применение слоистых геомодификаторов (глин, слюд) при создании функциональных материалов на основе полимерных матриц [18-21, 23, 25-27, 37].

Дата добавления: 2014-12-27