Кроме измеренного значения физической величины должна указываться и возможная величина ошибки

Поскольку истинное значение измеряемой величины в формуле (I) неизвестно, неизвестна и ошибка измерения δx. Для измерения возможной величины ошибки δx вводится понятие погрешности ∆ x.

Погрешность ∆ x измерения – это количественная мера неизвестной экспериментатору ошибки измерения δx. Количественно ∆ x можно задать как наибольшую по модулю ошибку так, чтобы выполнялось неравенство:

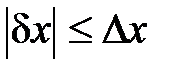(2)

Тогда из (1) и (2) следует, что истинное значение измеряемой величины лежит в интервале:

x _изм. – ∆ x ≤ x _ист. ≤ x _изм. + ∆ x (3)

Опыт, однако, показывает, что нерационально, а часто невозможно выбирать ∆ x столь большим, чтобы равенства (2) и (3) выполнялись абсолютно надёжно. Действительно, чем больше ∆ x, тем менее ценным является результат. Например, результат измерения длины маятника 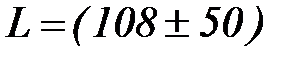см, несомненно, надежней результата 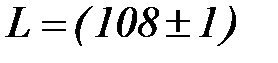см, однако ценность первого результата, конечно, ниже ценности второго. Поэтому величину ∆ x задают так, чтобы неравенства (2) и (3) выполнялись с некоторой вероятностью, Р. В учебных лабораториях принимают Р = 0,95. Это означает, что при многократном повторении опыта в одних и тех же условиях в среднем в 95 случаях из 100 ошибки не превысят ∆ x.

Основная задача физического измерения состоит в том, чтобы указать интервал, внутри которого с заданной наперёд вероятностью находится истинное значение искомой величины.

Интервал значений величины x, заданный соотношением (3), называется доверительным интервалом, а вероятность Р – доверительной вероятностью или надежностью, соответствующей этому доверительному интервалу.

По способу учёта в лабораторном практикуме погрешности делятся на 4 типа: поправки – ∆ x _попр., погрешности разброса – ∆ x _разб., приборные погрешности –
∆ x _пр., погрешности отсчёта и округления – ∆ x _окр..

Поправки вводятся тогда, когда известна или найдена величина и знак систематической ошибки. Например, если известна неточность градуировки прибора (указана в паспорте или графике поправок),то на неё вводится поправка.

Погрешности разброса учитывают те случайные ошибки, которые приводят к разбросу результатов около некоторого среднего значения при многократном повторении опыта в неизменных условиях.

К погрешностям разброса можно отнести также погрешности, связанные с грубостью принятой математической модели. Например, достаточно точные измерения длины реального стола дадут разные результаты в разных местах, так что если в качестве модели для реального стола принимаем модель прямоугольника с определёнными длиной и шириной, то различие значений длины и ширины в разных местах следует принимать как наличие погрешностей разброса.

Погрешности приборов учитывают неизвестные экспериментатору систематические ошибки конкретного прибора, связанные с его конструктивными особенностями.

Погрешности отсчёта и округления учитывают те случайные ошибки, которые вызваны несовершенством органов чувств экспериментатора и округлением результатов.

Величина погрешности ∆ x (она называется абсолютной) не всегда удобна для характеристики точности измерений и получаемых результатов. Например, если абсолютная погрешность измерения длины мм, а измеряемая длина составляет несколько метров, то точность измерения хорошая, а если измеряемая длина всего несколько миллиметров, то точность будет уже плохой. В связи с этим, так же из-за неудобства сравнения точности измерения разных величин, например, длины и времени, вводят относительную погрешность измерения, которую обычно выражают в процентах.

или (4)

б) Погрешности прямых измерений.

Будем считать далее, что поправки на известную систематическую погрешность уже учтены. Единичное измерение величины называется наблюдением.

Пусть произведено n наблюдений величины x в неизменных условиях и получены результаты x ₁, x ₂ … x _n. В качестве наиболее вероятного значения величины x принимается среднее арифметическое значений, найденное в отдельных наблюдениях:

(5)

Пусть случайное отклонение результата i-го измерения от среднего, то величину

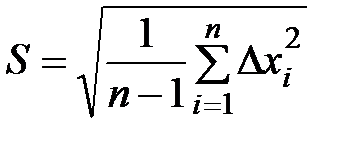(6)

называют средней квадратичной погрешностью отдельного наблюдения.

В теории вероятностей и математической статистике доказывается, что случайные отклонения результатов отдельных наблюдений от среднего, то есть ∆ x _i, в хорошо проведённом опыте не должны превосходить 3S. Если в каком-то наблюдении получено ∆ x _i > 3S, то это наблюдение должно считаться промахом.

Величина

(7)

называется средней квадратичной погрешностью всей серии n наблюдений. В математической статистике доказывается, что погрешность разброса связана с S_n соотношением

∆ x _разбр. =t_n,P S_n (8)

где множитель t_n,P называется коэффициентом Стьюдента. Индекс n у коэффициента указывает число опытов, а индекс Р – доверительную вероятность. Поскольку в лабораторном практикуме принята доверительная вероятность

Р = 0,95, то приведем значения коэффициентов t _n;0,95 для этой вероятности.

n
tn;0,95	1,60	0,82	0.77	0,74	0,73	0,72	0,71	0,71	0,70

Из таблицы видно, что чем больше проведено измерений, тем уже доверительный интеграл, то есть тем точнее измерения.

Погрешность прибора ∆ x_пр в прямых измерениях учитывается следующим образом. Для каждого типа приборов предприятие-изготовитель гарантирует на уровне доверительной вероятности P = 0,997 некоторую предельную погрешность ∆ _пред. Значения ∆ _пред для наиболее часто используемых мер и приборов указаны в таблице, находящейся в лаборатории. Поскольку в учебной лаборатории ограничивается значением доверительной вероятности P = 0,95, то принимается

∆ x _пр = 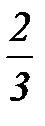∆ _пред (9)

Погрешность отсчёта и округления ∆ x _окр при доверительной вероятности P = 0,95 может быть принята равной половине цены деления шкалы прибора при округлении до целого деления и 0,3 от цены деления h при округлении до половины деления. Полная абсолютная погрешность прямого измерения рассчитывается по формуле:

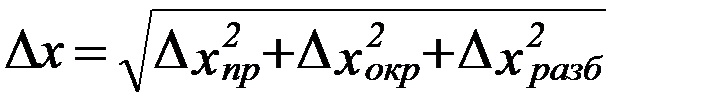(10)

Возможны, конечно, ситуации, когда погрешность какого-то типа значитель­но меньше остальных или вообще в эксперименте отсутствует. Например, если стол является четырехугольником, длины сторон которого отличаются меньше, чем на 0,1 мм, то при использовании в качестве его модели квадрата, стороны которого измеряются линейкой с миллиметровыми делениями, погрешность разброса будет вообще отсутствовать, ибо они замаскированы погрешностями отсчета и округления, которые составляют в данном случае 0,5 мм. Считается, что четверть миллиметровых делений глаз среднего человека отсчитать не в состоянии, а погрешность линейки, если она металлическая длиной 1000 мм, можно не учитывать, ибо она составляет лишь 0,2 мм.

Окончательный результат записывается в виде:

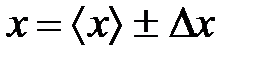(11)

и имеет надёжность на уровне P = 0,95

в) Погрешности косвенных измерений.

При косвенных измерениях интересующая нас физическая величина y задается как функция прямым образом изменяемых физических величин x ₁, x ₂ … x _n; y = f ( x ₁, x ₂ … x _n). Наиболее вероятное значение величины y, то есть результат косвенного измерения, находится следующим образом:

(12)

Поскольку каждая из величин (i = 1, 2, 3,..., n) определена с погрешностью ∆x_i, то и величина y_изм, вычисленная по формуле (12) также будет найдена с некоторой погрешностью, которая вычисляется по формуле:

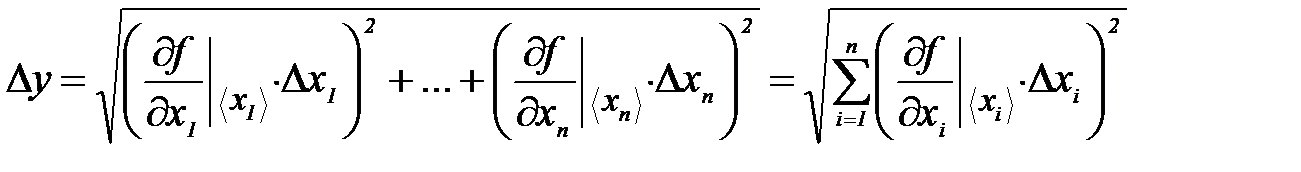, (13)

где 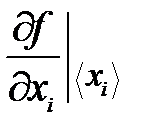– частные производные функций (12) по аргументам, вычисленным при средних значениях. Доверительная вероятность для погрешности ∆ y будет равна Р = 0.95 при условии, что она имеет такое значение для каждой из погрешностей ∆ x_i.

Относительная погрешность косвенной величины у равна:

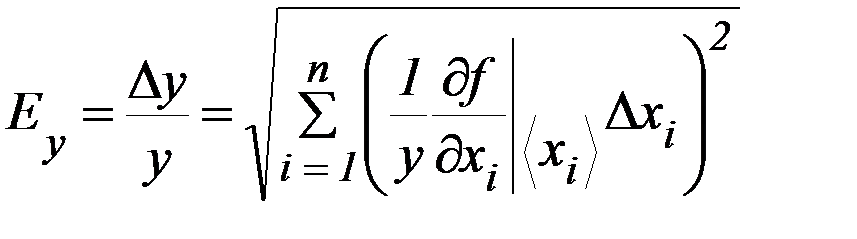(14)

Поскольку вычисление погрешностей часто достаточно громоздко, иногда используются более простые правила, которые, вообще говоря, иногда несправедливы, но в большинстве случаев могут быть в лабораторном физпрактикуме использованы. Например, можно принять, что относительная погрешность косвенной физической величины в 1,5 раза больше максимальной относительной погрешности всех прямым образом измеряемых величин. Поэтому в эксперименте следует стремиться к тому, чтобы относительные погрешности всех прямым образом измеряемых величин были примерно одинаковы. Для величин, значения которых зависят от выбора начала отсчета, например, координат, следует избегать появления близких к нулю значений, ибо при этом относительная погрешность велика.

г) Графическая обработка результатов.

Выбор координатных осей. По оси абсцисс всегда откладывается аргумент, по оси ординат – функция.

Выбор масштаба. При выборе масштаба необходимо придерживаться следующих рекомендаций:

1. Шкалы на всех осях должны легко читаться, поэтому одна клеточка миллиметровой бумаги должна соответствовать удобному числу единиц измеряемой величины (1, 2, 5, 10….).

2. Экспериментальные точки не должны сливаться друг с другом.

3. Масштабы вдоль осей следует выбирать так, чтобы основная часть графика имела наклон, близкий к 45º, и лежала в средней части между осями.

4. Если на графике необязательно иметь начало координат, начало, и конец разметки по осям должны соответствовать минимальным и максимальным значениям аргумента и функции.

5. Десятичные множители удобнее отнести к единице измерения, тогда деления на осях будут помечены цифрами 1; 2; 3 и т. д., а не 10000; 20000 или 0,001; 0,002.

Построение графиков. На график наносятся все полученные в измерениях точки (выносные линии не проводятся). Через экспериментальные точки проводится наилучшая плавная кривая. Непосредственное соединение экспериментальных точек ломаной линией не допускается. Точки должны располагаться как можно ближе к кривой так, чтобы по обе стороны от неё находилось по возможности одинаковое число точек.

Нанесение ошибок на график. Ошибка в экспериментальном значении указывается в виде крестиков, размеры которых в выбранном масштабе дают удвоенное значение погрешностей в этом масштабе. Кривая графика должна пересекать прямоугольники, образованные крестиками погрешностей.

Дата добавления: 2014-12-27