
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Подготовка прибора к работе и проведение измерений. Цель работы: изучение законов поступательного и вращательного движения для определения моме
Описание установки
НА МАШИНЕ АТВУДА
ПОСТУПАТЕЛЬНОГО И ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
ИЗУЧЕНИЕ ЗАКОНОВ И ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК
Лабораторная работа М 2
Цель работы: изучение законов поступательного и вращательного движения для определения момента сил трения (Мтр).
Приборы и принадлежности:
– установка с машиной Атвуда;
– набор перегрузков кольцеобразной формы.

| 7,8 |
Рисунок 1 – Общий вид установки
Общий вид машины Атвуда показан на рисунке1. На вертикальной колонне (1) расположены три кронштейна: нижний кронштейн (2) неподвижен, а кронштейны (3) и (4) могут перемещаться вдоль колонки и фиксироваться в любом положении стопорными винтами. Расстояние между кронштейнами может быть найдено с помощью миллиметровой шкалы на колонке. В верхней части колонки находится блок (5), через который перекинута нить (6) с привязанными на её концах грузами (7) и (8) одинаковой массы, винты для горизонтирования установки (9). В экспериментальной установке имеется три перегрузка кольцеобразной формы различной массы, которые можно класть порознь, по два вместе и, наконец, все три вместе.
Установка работает следующим образом: устанавливаются необходимые расстояния между нижним и средним кронштейнами (S2) и верхним и средним кронштейнами (S1). Нажимается кнопка «СЕТЬ». При этом специальный электромагнит препятствует свободному вращению блока. На правый груз кладётся один или несколько перегрузков кольцеобразной формы, которые имеются в комплекте. Груз с прегрузком рукой устанавливается в положение, когда его нижняя грань совпадает с чертой на верхнем кронштейне. В этом положении груза нажимается кнопка «ПУСК». Когда правый груз с перегрузками достигает среднего кронштейна, перегрузки снимаются, и специальный фотоэлектрический датчик включает секундомер. Когда правый груз достигает нижнего кронштейна с другим фотодатчиком, то секундомер выключается. Для продолжения измерений нажимается кнопка «СБРОС», подготавливая секундомер для дальнейших измерений. Отжимается кнопка «ПУСК».
Последующие измерения начинаются с установки правого груза с перегрузком в исходное положение, описанное выше. Устраняются колебания грузов. Нажимается кнопка «ПУСК» и т. д. Возможно, при движении правого груза он задевает кольцо на среднем кронштейне, предназначенное для снятия перегрузков, и дальнейшее движение грузов сопровождается колебаниями. Возможно также, что правый груз не попадает в приемное окно нижнего кронштейна. Для проведения измерений эти эффекты нужно устранить!
Это достигается горизонтированием установки с помощью винтов (9)и небольшим поворотом в горизонтальной плоскости среднего кронштейна (3).
В дальнейшем изложении будем использовать следующие обозначения:
Мтр – момент силы трения; [Mтр] = Н×м;
m – массы грузов, висящих на нити, перекинутой через блок; [m] = кг;
∆m – масса перегрузка, который кладётся на правый груз; [∆m] = кг;
S1 – расстояние между верхним и средним кронштейнами, т. е. путь, который проходит груз вместе с перегрузком; [S1] = м;
S2 – расстояние между средним и нижним кронштейнами, т. е. путь, который проходит груз без перегрузка; [S2] = м;
t – время движения правого груза на этапе 2; [t] = сек;
а1 – ускорение правого груза на этапе 1; [a1] = м/с2;
а2 – ускорение правого груза на этапе 2; [a2] = м/с2
R – радиус блока; [R] = м.
Этап движения с перегрузком называется далее этапом 1, а этап движения без перегрузка – этапом 2.
Установка позволяет делать прямые измерения времени движения t правого груза на пути S2 между средним и нижним кронштейнами при различных задаваемых значениях масс перегрузков ∆m, перемещения S1 на этапе 1 и перемещения S2 на этапе 2.
Задание для самостоятельной работы.
Определение момента силы трения МТР.
1. Выберете любое значение S1 в интервале от 6 до 15 см. Установите минимальное возможное значение S2 (S2 ≥ 5 см).
2. Измерьте не менее трёх раз время движения правого груза на этапе 2, используя на этапе 1 перегрузок кольцеобразной формы ∆m. Найдите среднее время движения t.
3. Теория даёт следующую систему уравнений для поступательного движения грузов и вращательного движения блока на этапе 1 (см. Приложение):
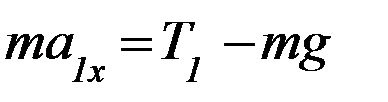 (1)
(1)
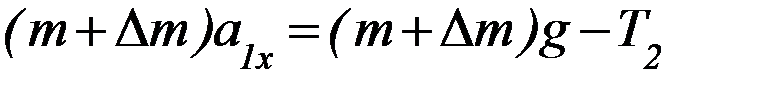 (2)
(2)
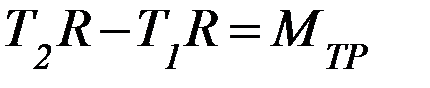 (3)
(3)
Получить математическое выражение для ускорения правого груза на этапе 1 (a1x –?) из системы уравнений 1 – 3.
4. Теория даёт следующую систему уравнений для поступательного движения грузов и вращательного движения блока на этапе 2 (см. Приложение):
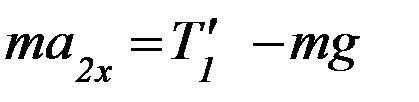 (4)
(4)
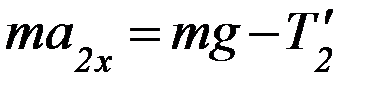 (5)
(5)
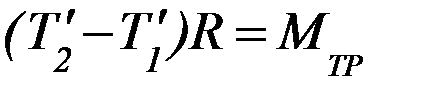 (6)
(6)
Получить математическое выражение для ускорения правого груза на этапе 2 (a2x –?) из системы уравнений 4 – 6.
5. Получить следующее математическое выражение для пути (7), проходимого правым грузом (без перегрузка), используя для этого уравнения кинематики и результаты заданий 2, 3 и 4:
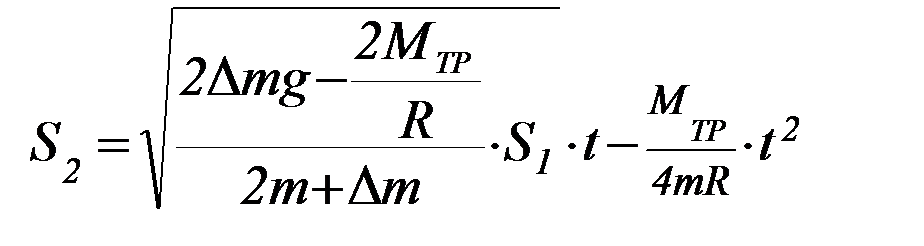 (7)
(7)
6. Из полученного выражения (7), подставив измеренное в задании 1 время t и все остальные известные параметры, найти момент силы трения МТР.
7. Рассчитать относительную погрешность определения момента силы трения.
Из-за сложности математического выражения для определения момента силы трения можно воспользоваться упрощённым вариантом расчёта погрешности Мтр. Для этого относительные погрешности прямым образом определяемых величин (m, t, S) принять равными: 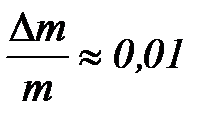 ;
; 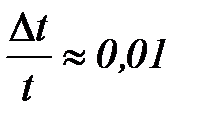 ;
; 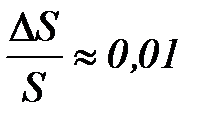 .
.
Рассчитать относительную погрешность определения момента силы трения как сумму относительных погрешностей прямым образом определяемых величин (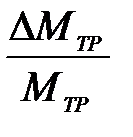 ).
).
Приложение. Законы динамики вращательного и поступательного движений.
Рассмотрим блок радиуса R с моментом инерции J, который может вращаться вокруг горизонтальной оси (рисунок 2).
Через блок перекинута невесомая, нерастяжимая нить, на концах которой висят грузы массой m каждый. Если на один из грузов (на рисунке – на правый) положить перегрузок достаточно большой массы ∆m, система придёт в движение (разумеется, при отсутствии сил трения перегрузок сколь угодно малой массы приводит систему в движение, но при наличии сил трения это не так). Найдём ускорения грузов, считая, что при движении нить по блоку не сколь 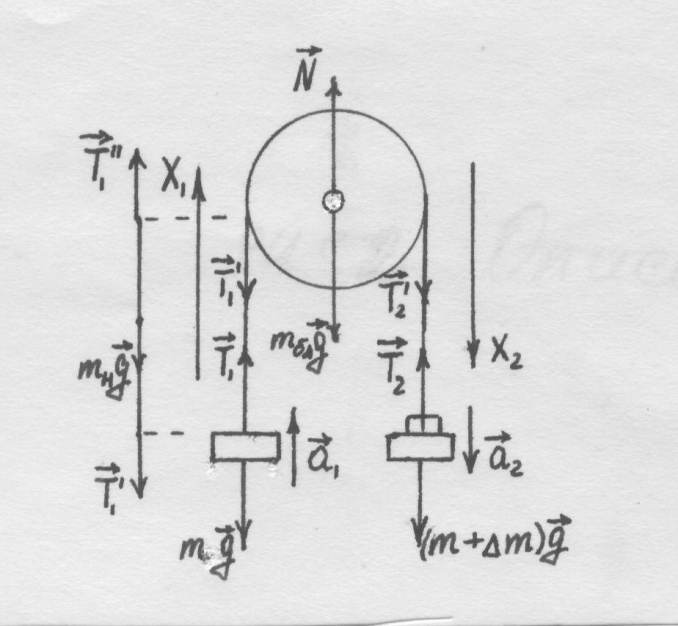 зит. Будем считать, что диссипативные силы, зависящие от скорости (например, силы сопротивления воздуха) отсутствуют. На левый груз действует сила тяжести
зит. Будем считать, что диссипативные силы, зависящие от скорости (например, силы сопротивления воздуха) отсутствуют. На левый груз действует сила тяжести 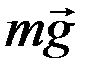 и сила
и сила 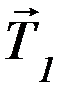 со стороны нити. На левый вертикальный участок нити действуют две силы: сила
со стороны нити. На левый вертикальный участок нити действуют две силы: сила 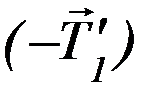 со стороны левого груза, которая по III закону Ньютона равна силе
со стороны левого груза, которая по III закону Ньютона равна силе 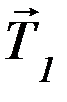 по модулю и противоположна по направлению, и сила
по модулю и противоположна по направлению, и сила  со стороны участка нити, находящегося на блоке. На рисунке слева отдельно показан левый участок нити и силы, на него действующие; напомним, что нить считается невесомой. Запишем второй закон Ньютона для левого участка нити:
со стороны участка нити, находящегося на блоке. На рисунке слева отдельно показан левый участок нити и силы, на него действующие; напомним, что нить считается невесомой. Запишем второй закон Ньютона для левого участка нити:
| Рисунок 2 – Блок с грузами |
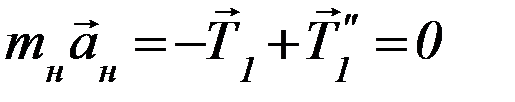 , поскольку mнити = 0
, поскольку mнити = 0
Тогда, 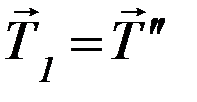 . По третьему закону Ньютона сила
. По третьему закону Ньютона сила 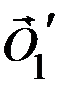 , с которой левый вертикальный участок нити действует на участок, находящийся на блоке, равна
, с которой левый вертикальный участок нити действует на участок, находящийся на блоке, равна
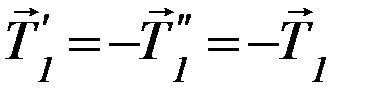
Фактически, сила 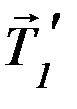 оказывается приложенной к блоку, поскольку в отсутствие проскальзывания блок и участок нити, находящийся на нём, составляют единое целое.
оказывается приложенной к блоку, поскольку в отсутствие проскальзывания блок и участок нити, находящийся на нём, составляют единое целое.
Аналогичные рассуждения применимы и для правого вертикального участка нити. Для модулей сил, следовательно, имеем
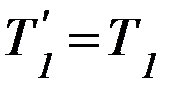 и
и 
Запишем систему уравнений, описывающих поступательное движение обоих грузов. Для этого выберем положительное направление осей Х1 и Х2 так, чтобы они совпадали с направлением движения тел (такой выбор осей называется согласованным).
Тогда для висящих грузов, которые движутся поступательно, второй закон Ньютона при движении тел на первом этапе (S1):
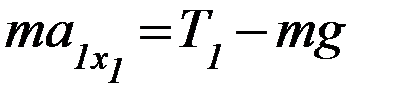 (П-1)
(П-1)
 (П-2)
(П-2)
Вследствие нерастяжимости нити модули перемещений грузов на обоих концах нити одинаковы. Одинаковы модули скоростей и ускорений грузов, но направления их, конечно, противоположны:
 ,
,
где а – модуль ускорения каждого груза.
При этом  ускорения грузов на этапе I.
ускорения грузов на этапе I.
Рассмотрим теперь силы, которые действуют на блок. Помимо силы тяжести 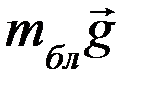 , сил
, сил 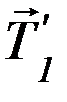 и
и 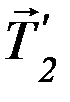 , о которых шла речь выше, на блок действует сила реакции оси
, о которых шла речь выше, на блок действует сила реакции оси 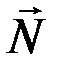 , а также силы трения в оси блока. Детальный анализ сил трения очень сложен, поэтому ограничимся рассмотрением упрощённой модели, которая достаточно хорошо подтверждается опытом. Для вращения блока существенны не сами силы трения, а их моменты относительно оси вращения. Поскольку центр масс блока покоится, то
, а также силы трения в оси блока. Детальный анализ сил трения очень сложен, поэтому ограничимся рассмотрением упрощённой модели, которая достаточно хорошо подтверждается опытом. Для вращения блока существенны не сами силы трения, а их моменты относительно оси вращения. Поскольку центр масс блока покоится, то 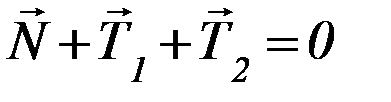 . Переходя к модулям сил, получим:
. Переходя к модулям сил, получим:
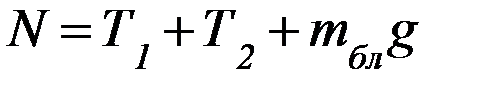 .
.
Запишем для блока основное уравнение динамики вращательного движения
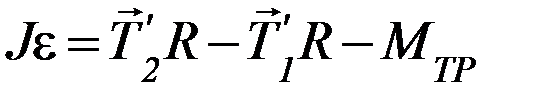 (П-3)
(П-3)
Если блок невесом, то Jбл. = 0 и 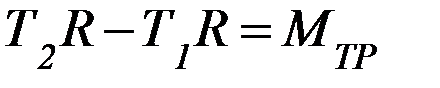
Если нить по блоку не скользит, то модуль скорости грузов равен модулю линейной скорости точек на окружности блока:
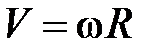
Дифференцируя это соотношение по времени, получим следующую связь модуля ускорений грузов а и углового ускорения ε:
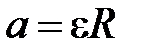
Тогда (П-3) можно переписать в виде
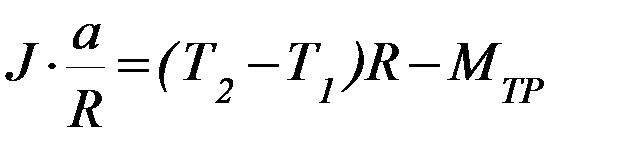 (П-4)
(П-4)
Решая систему уравнений (П-1), (П-2), (П-4), получим выражение для модуля ускорений грузов при движении и на первом этапе
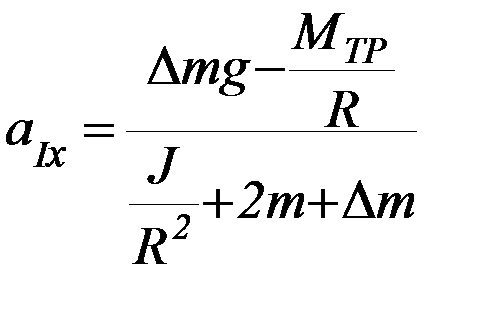 (П-5)
(П-5)
Если блок невесом: 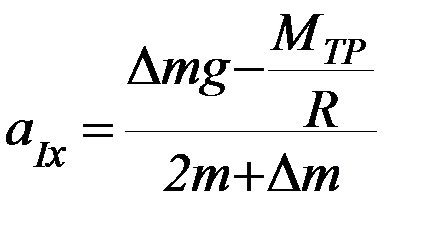 (П-6)
(П-6)
Если система некоторое время движется с ускорением аIх на этапе 1, а затем перегрузок снимается, то дальнейшее движение системы на этапе 2 будет происходить с ускорением аIIх, выражение для которого вытекает из формулы (П-6) при ∆m = 0:
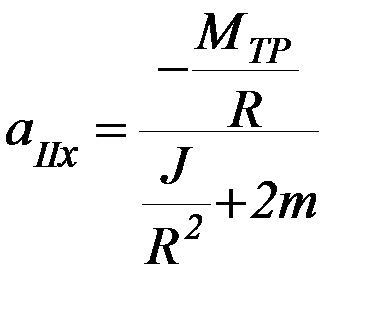 (П-7)
(П-7)
Если блок невесом: 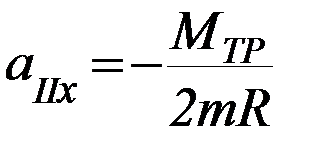 (П-8)
(П-8)
Знак «минус» показывает, что движение вследствие наличия сил трения будет замедленным.
Аналогичное выражение для ускорения аIIx можно получить, если записать законы поступательного и вращательного движения на этапе 2 в отсутствие перегрузка и невесомости блока:
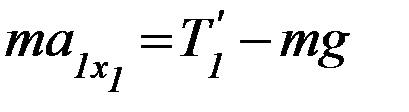 (П-9)
(П-9)
 (П-10)
(П-10)
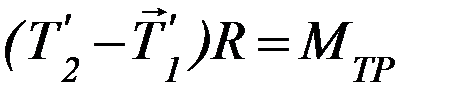 (П-11)
(П-11)
где 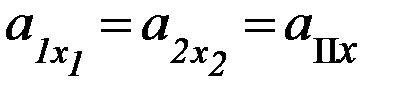
В работе правый груз проходит с перегрузком задаваемый экспериментатором путь S1 (этап 1), а затем перегрузок снимается и измеряется время движения на пути S2, который тоже задаётся экспериментатором (этап 2). Поскольку во всех случаях ускорения аIх и аIIx – постоянные величины, справедливы все известные из школьного курса физики формулы кинематики.
В частности, поскольку движение с перегрузком начинается без начальной скорости, скорость правого груза в конце этапа 1 (она же является начальной скоростью на этапе 2) связана с путём S1 соотношением:
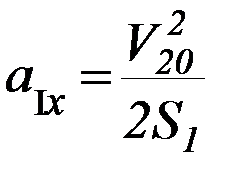 (П-12)
(П-12)
Время движения t на этапе 2 связано с выражением для пути S2 формулой:
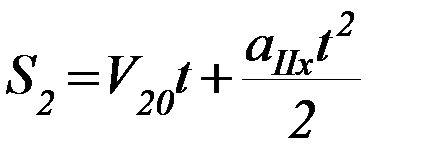 (П-13)
(П-13)
Если массой блока можно пренебречь, то при подстановке формул (П-6), (П-8), (П-12) в (П-13) получим следующее выражение для определения момента сил трения:
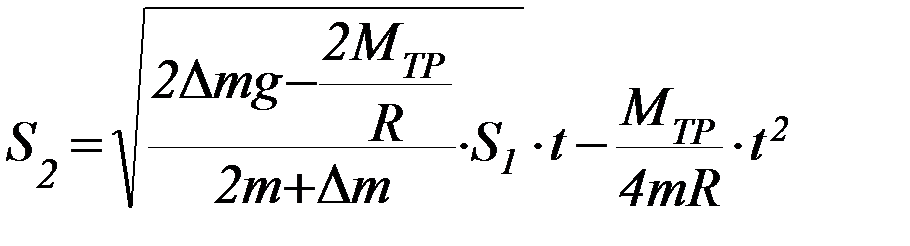 (П-14)
(П-14)
Контрольные вопросы:
1. Сформулируйте основные законы динамики поступательного и вращательного движения.
2. Определите скорости грузов в конце заданного перемещения на основе закона сохранения механической энергии.
3. Определите массу блока, зная его радиус, S1, S2 и измеряя время движения на этапе 2. (Используйте теорию Приложения).
4. Определите момент инерции блока, измерив его радиус и положение отверстий на нём.
5. Напишите уравнение движения грузов, если в оси блока есть трение.
6. Допустим, что нить имеет массу. Напишите уравнение движения грузов для этого случая.
|
|
Дата добавления: 2014-12-27; Просмотров: 1270; Нарушение авторских прав?; Мы поможем в написании вашей работы!