Описание установки

Оси на маятнике обербека

Движения твердого тела вокруг неподвижной

Изучение законов динамики вращательного

Лабораторная работа М 5

Цель работы:

– экспериментальная проверка зависимостей между физическими величинами, характеризующими вращение твердого тела вокруг неподвижной оси.

Приборы и принадлежности:

– маятник Обербека; комплект перегрузов; миллисекундомер.

Рисунок 1 – Общий вид установки

Маятник Обербека представляет собой крестовину, на оси которой закреплены два блока радиусами r₁ и r₂. На диски может наматываться нить, причём один конец нити прикрепляется к диску, а на другой подвешен груз m₁, состоящий из основного груза, на который могут помещать добавочные грузы. Поступательное движение груза вниз вызывает вращательное движение крестовины с блоками вокруг неподвижной горизонтальной оси. На четырех взаимно перпендикулярных стержнях симметрично расположены грузы массой m. Их можно установить на любом заданном расстоянии r от оси вращения. Маятник с помощью неподвижного кронштейна установлен на вертикальной колонне, на которой нанесена миллиметровая шкала для подсчета длины перемещения грузов. На вертикальной колонне (1) прикреплены два кронштейна: нижний (2) неподвижный и верхний (3) подвижный. Подвижный кронштейн (3) можно перемещать вдоль колонны (1) и фиксировать его в любом положении, задавая таким образом расстояние Н, которое проходят грузы. Установка снабжена двумя фотоэлектрическими датчиками (4 и 5), вырабатывающими электрические импульсы соответственно начала и конца измерения времени движения грузов. Маятник с грузами удерживается в состоянии покоя с помощью тормозного электромагнита. На основании колонны жестко закреплен миллисекундомер (6), к которому подключены фотодатчики. Само основание прибора снабжено регулируемыми ножками (7), обеспечивающими горизонтальную установку прибора.

На установке можно провести прямое измерение времени движения груза массой m₁ на пути Н и получить таким образом множество значений времени при различных m₁, H, r и радиусах намотки r₁ и r₂ и различных положениях грузов m.

Ясно, что проведение измерений времени при всех возможных комбинациях указанных величин – нереальная задача. Кроме того, неясно, что с результатами делать дальше и что с их помощью можно определить.

Ответы на последние вопросы дает теоретическая модель экспериментальной ситуации. Она же позволяет составить план измерений и обработки результатов.

Любая теоретическая модель дает приближенное описание экспериментальной ситуации, поскольку пренебрегает влияниям многих реально имеющих место эффектов.

Внимание! Для отчета по работе необходимо изучить также материал приложений.

В этой модели считается, что трение в оси блока (8) отсутствует, этот блок невесом, а момент сил трения Μ_тр, в оси блока с крестовиной не зависит от угловой скорости вращения. В этих условиях ускорение груза массой m постоянно на всем отрезке Н и равно:

,

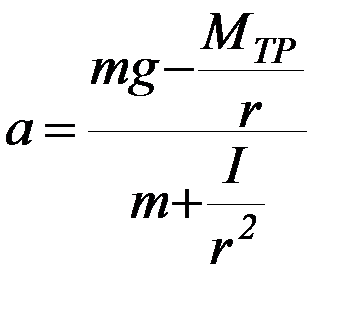где r – радиус намотки, I – момент инерции блока с крестовиной (r = r₁ либо r₂,

I – определяется положением грузов массой m каждый и моментом инерции блока без грузов I_о ().

С другой стороны, на основании кинематических соображений, если а – постоянная величина, то ,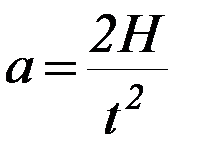

где Н – задаваемое перемещение груза, t – измеренное время его движения.

Имеем: (1)

Тогда формула (1) является основной для работы в рамках теоретической модели.

Задание 1. Определить момент инерции (Io) крестовины без грузов.

1. Освободите стержни крестовины от грузов m и убедитесь, что блок с крестовиной находится в безразличном равновесии в любом из возможных положений, когда нить с грузом m не прикреплена к блоку. Если это не так, то добейтесь состояния безразличного равновесия путем незначительного ввинчивания или вывинчивания стержней крестовины в ось блока.

2. Измерьте время движения груза m₁ c высоты H. Измерения сделать 3 раза и усреднить;

3. Рассчитайте экспериментальное значение ускорения груза m₁ по формуле

(1)

Запишем второй закон Ньютона для поступательного движения груза m₁ и вращательного движения для крестовины без грузов (см. Приложение).

x

m₁g

H

T

m₁

ε

R

m₁a_x = m₁g – T, (2)

I_oe = TR

где e – угловое ускорение вращения крестовины;

Т – сила натяжения нити;

R – радиус намотки нити.

Поскольку нить по блоку не скользит, то: e = а/R, тогда из системы уравнений (2) получим теоретическое значение ускорения груза m₁:

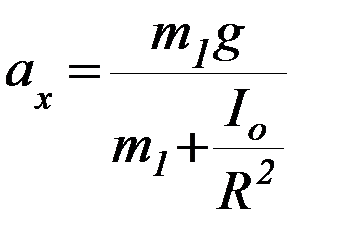(3)

Приравняв теоретическое (3) и экспериментальное (1) выражения для ускорения груза m₁, получим следующее равенство:

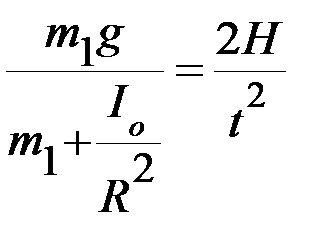(4)

4. Из равенства (4) выразите и рассчитайте момент инерции I_o крестовины без грузов.

Повторите пункты 2) – 4) при различных значениях H и m₁. Полученные значения I_o усредните.

5. Рассчитайте погрешность определения момента инерции по формуле:

Погрешности прямым образом измеренных величин принять равными:

∆m = 0,1 г; ∆R = 1 мм; ∆t = 0,005 сек; ∆H = 0,5 мм.

ρ

m

m

m

m

m₁

Задание 2. Определить момент инерции (I) крестовины с закреплёнными на ней грузами m.

1. Закрепите грузы m на указанном преподавателем расстоянии (ρ) от оси и опять проверьте, находится ли система в состоянии безразличного равновесия. Если это не так, небольшими смещениями грузов на стержнях крестовины добейтесь, чтобы это состояние имело место.

2. Установите кронштейн с верхним фотодатчиком на минимальное значение Н из рабочего интервала.

3. Закрепите один конец диска нити на диске радиуса R = r₁ или R = r₂ по указанию преподавателя, перекиньте нить с подвешенным на другом её конце грузом (основной груз + указанное преподавателем число добавочных грузов) через неподвижный блок и добейтесь, чтобы нижний край груза m₁ совпал с чертой на корпусе верхнего фотодатчика.

4. Измерьте время движения груза m₁ c высоты H. Измерения сделать 3 раза и усреднить;

Из равенства теоретического и экспериментального значения ускорения (формула 5) найдите и рассчитайте момент инерции (I =?) крестовины с закреплёнными на ней грузами массой m:

(5)

Повторите пункты 1) – 4) при разных значениях r. Полученные значения I усредните.

5. Посчитайте теоретическое значение момента инерции по формуле 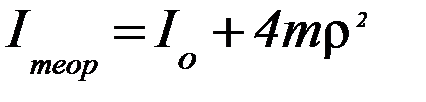(6):

(6)

6. Оцените относительную погрешность измерений по формуле (7):

(7)

Приложение. Основные сведения по динамике вращательного движения твердого тела вокруг неподвижной оси.

Движение твердого тела, при котором две его точки остаются неподвижными, называется вращением тела вокруг неподвижной оси. Прямая, соединяющая эти точки, называется осью вращения тела. При вращении вокруг неподвижной оси все точки тела описывают окружности, центры которых лежат на оси вращения, а плоскости перпендикулярны к ней. Положение твердого тела в пространстве полностью определяется значением φ угла поворота тела из некоторого начального положения.

Для характеристики быстроты вращения тела вокруг оси служит угловая скорость. Угловой скоростью называется быстрота изменения (точнее, производная) угла поворота φ по времени:

(П-1)

Вращение считается равномерным, если ω = const.

Величиной, характеризующей быстроту (и направление) изменения угловой скорости, является угловое ускорение. Производная от угловой скорости или вторая производная угла поворота по времени

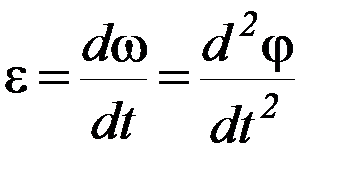(П-2)

Модуль угловой скорости и углового ускорения связаны соответственно с модулями линейной скорости V и линейного ускорения a соотношениями:

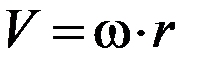, , (П-3)

где r – радиус окружности вращения.

Моментом силы относительно неподвижной точки (полюса) называется векторная величина , равная векторному произведению радиус-вектора 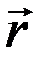, проведенного из этой точки в точку приложения силы, на вектор силы :

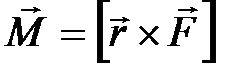(П-4)

Модуль момента силы:

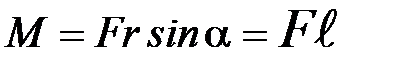, (П-5)

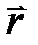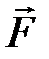где – угол между векторами и , а 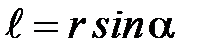– плечо силы.

При переносе точки приложения силы вдоль линии её действия момент этой силы относительно одной и той же неподвижной точки не изменяется. Если линия действия силы проходит через точку вращения, то момент силы относительно этой точки равен нулю.

Моментом силы 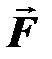относительно неподвижной оси OZ называется скалярная величина М_z, равная проекции на эту ось вектора момента силы 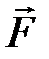относительно произвольной точки на оси. Значение М_z, не зависит от выбора положения точки на оси.

Главный момент относительно неподвижной оси системы сил равен алгебраической сумме моментов относительно этой оси всех сил.

Моментом инерции математической системы относительно неподвижной оси OZ называется физическая величина I_z, равная сумме произведений масс всех N материальных точек на квадраты расстояний до оси OZ:

, (П-6)

где m_i и ρ_i – масса i -ой точки и ее расстояние от оси.

Дата добавления: 2014-12-27