Геометрическим изображением СО является система координат (СК)

Простейшим вариантом СК является, декартова прямоугольная система координат. Движение частицы в этой системе координат может быть задано разными способами. Наиболее распространенный из них – это так называемый кинематический закон движения, когда задаются зависимости от времени всех координат частицы:

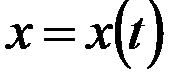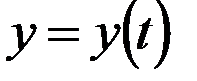, , (15)

Вводя в рассмотрение радиус-вектор частицы 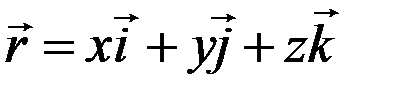, идущий из начала координат в рассматриваемую точку, можно уравнение (15) записать в векторном виде

(16)

Здесь, , , 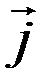– орты координаты осей. Выражения (15), (16) называются кинематическим законом движения точки.

Траекторией точки в данной СО называется кривая, описываемая точкой при движении. Уравнение траектории получается из уравнения (16) путём исключения времени t. Вектором перемещения за промежуток времени 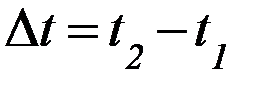называется вектор, равный (см. рисунок 2)

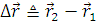(17)

Путь , пройденный точкой за промежуток времени 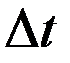, определяется как длина дуги между точками 1 и 2.

(18)

Вектором средней скорости называется величина (рисунок 2)

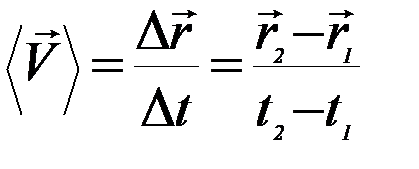(19)

Направлен вектор 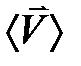так же, как и .

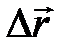Здесь знак «» называется равенством по определению, чтобы отличать его от знака равенства, стоящего в физических законах. Векторы скорост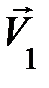и и начинаются в тех точках, в которых находилась частица в соответствующие моменты времени, а вектор скорости 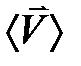, характеризующий движение частицы в интервале времени 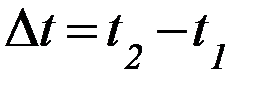, можно рисовать в любой точке траектории, соответствующей указанному интервалу (на рисунке 2 он изображен в точке, соответствующей моменту t₂).

касательная

касательная

Рисунок 2 – Траектория движения материальной точки

Вектор мгновенной скорости характеризует быстроту измерения радиус – вектора точки в данный момент времени и определяется равенством:

(20)

Проекции этого вектора на координатные оси равны:

; ;

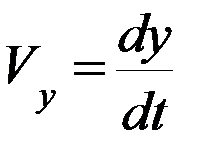Тогда

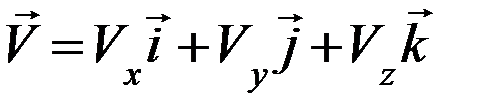(21)

и модуль вектора скорости:

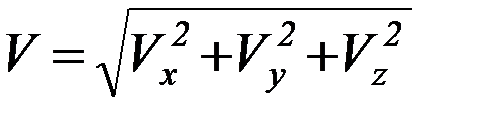(21)*

Вектор направлен по касательной к траектории в сторону движения точки (рисунок 2). Движение точки можно задать и иначе: задается уравнение траектории, положение точки на траектории в начальный момент времени t = 0 и зависимость пройденного пути от времени . Такой способ задания движения принято называть естественным. Тогда модуль вектора скорости определяется равенством:

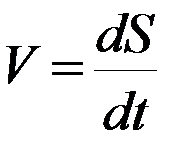, (22)

а сам вектор записывается в виде: ,

где 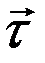– единичный вектор касательной , (23)

Направляющие косинусы вектора скорости:

; ; (24)

Вектор среднего ускорения определяется равенством (рисунок 3)

(25)

Рисунок 3 – Вектор среднего ускорения

Вектор мгновенного ускорения 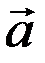характеризует быстроту изменения вектора скорости в данный момент и определяется соотношением:

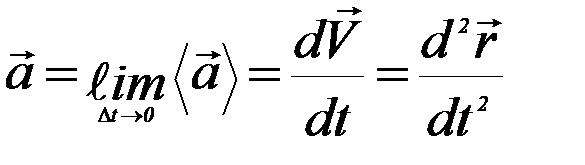(26)

Проекции вектора ускорения на координатные оси:

; ; (27)

Тогда

(28)

модуль вектора ускорения

(29)

Дата добавления: 2014-12-27