Связанных колебательных контуров

Передаточные частотные характеристики

Рассмотрим схему передачи энергии гармонических воздействий от источника Е ₁ в нагрузку R _н в СКК с трансформаторной связью двух одинаковых ОКК, в которых используются переменные конденсаторы для обеспечения их настроек (рис. 4.20). Обозначим R ₁ = R_i + R и R ₂ = R + R _н.

Рассмотрим передаточную характеристику СКК как отношение тока во вторичном контуре I ₂ к напряжению источника Е ₁. Тогда с учетом (4.30) получим

. (4.36)

Максимальное значение функции H (jω) достигается в следующих случаях:

–настройка на резонансную частоту ω ₀ первичного ОКК;

–настройка на резонансную частоту ω ₀ вторичного ОКК;

–индивидуальная настройка на резонансную частоту ω ₀ каждого ОКК при отсутствии связи между ними;

–выбор оптимальной связи между ОКК.

В связи с этим различают следующие виды настроек СКК:

1) настройка первичного ОКК, при которой в СКК достигается первый частный резонанс:

Х _вх = X ₁₁ + X _вн1 =0; Z _вх = R _вх.

Согласно (4.36), ;

2) настройка вторичного ОКК, при которой в СКК достигается второй частный резонанс:

Х _вых = X ₂₂ + X _вн2 =0; Z _вых = R _вых.

Согласно (4.36), ;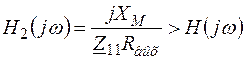

3) индивидуальная настройка каждого ОКК, при которой достигается индивидуальный резонанс:

X ₁₁ = X ₂₂ =0; X _вн1 = X _вн2 =0; Х _вх = Х _вых =0; Z ₁₁= R ₁,

т.е. Z _вх = R _вх и Z _вых = R _вых.

Согласно (4.36), ;

4) настройка на один из частных резонансов и выбор оптимальной связи изменением взаимной индуктивности M, при которой достигается сложный резонанс.

Из уравнения 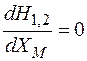получим

.

Тогда ;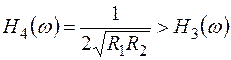

5) индивидуальная настройка ОКК и выбор оптимальной связи путем изменения взаимной индуктивности М, при которой достигается полный резонанс. Из уравнения 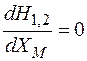получим

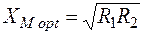. Тогда 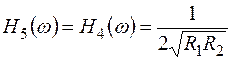. (4.37)

При анализе АЧХ СКК удобно использовать параметр связи (4.35):

.

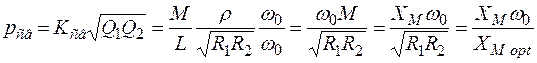Тогда 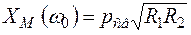. (4.38)

Таким образом, параметр связи – это отношение сопротивления связи на резонансной частоте к оптимальному сопротивлению связи.

При настройке ОКК (ξ = 0) из (4.33) получим

(4.39)

Таким образом, максимальное значение вносимых резистивных сопротивлений пропорциональна квадрату параметра связи.

Для удобства анализа рассмотрим СКК с одинаковыми ОКК, т.е. при R _l = R ₂ = R; ξ ₁= ξ₂ = ξ; Z ₁₁ = Z ₂₂ = Z = R (1+ jξ).

Из (4.36) с учетом (4.38) при Х _м ≈ Х _м (ω ₀) = р _св R получим

.

АЧХ СКК равна . (4.40)

Рассмотрим нормированную АЧХ СКК с учетом максимально возможного значения :

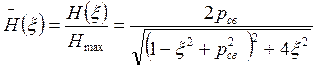. (4.41)

При настройке (ξ = 0)

(4.42)

Из условия H _н(ξ) = 1 определим значение обобщенной расстройки для частот максимума АЧХ (частот связи):

ξ_ч.c = 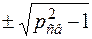. (4.43)

Из (4.43) следует:

– при р _св > 1 существуют две симметрично расположенные относительно ω ₀ (ξ= 0) частоты связи, т.е. нормированная АЧХ достигает максимума (значения 1) в двух точках (± ξ _{ч с}), т.е. становится «двугорбой» (рис. 4.21);

– при р _св = 1 две частоты связи «сливаются» в одну частоту ω ₀, т.е. нормированная АЧХ достигает максимума в одной точке (ξ = 0);

– при р _св < 1 действительных значений частот связи нет, т.е. нормированная АЧХ нигде не достигает максимума,.

Таким образом можно сделать следующие выводы:

1. При р _св > 1 АЧХ СКК является «двугорбой», причем «горбы» (максимумы) находятся на частотах связи ± ξ _{ч с}.

2. При р _св = 1 «одногорбая» АЧХ переходит в «двугорбую», поэтому параметр связи р _св = 1 называют критическим.

3.При р _св = 2,41 «провал двугорбой» АЧХ достигает уровня 0,7, ниже которого АЧХ не должна опускаться в полосе пропускания, иначе получим раздвоенную полосу пропускания, что недопустимо; поэтому параметр связи р _св = 2,41 называют предельным.

4. С увеличением р _св увеличивается коэффициент прямоугольности (избирательность) К _пр и достигает предельного значения 0,43 при предельном параметре связи

Дата добавления: 2014-12-27