Метод переменных состояния

Для расчета переходных процессов в цепях, содержащих три и более реактивных элемента, применяют метод переменных состояния, позволяющий сформировать систему дифференциальных уравнений в форме Коши (в нормальной форме) и решить ее операторным или численным методом.

В качестве переменных состояния электрической цепи выбирают токи i_L в индуктивностях и напряжения u_C на емкостях, т. е. те величины, которые определяют общий порядок системы дифференциальных уравнений. Эти величины задают в каждый момент времени энергетическое состояние электрической цепи, поэтому у метода есть такое название – метод переменных состояния.

Порядок составления уравнений следующий. Сначала записывают уравнения цепи по законам Кирхгофа, затем их преобразовывают путем исключения других переменных так, чтобы остались только переменные состояния, их производные и источники. Полученную систему уравнений записывают в матричной форме ,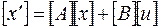

где ;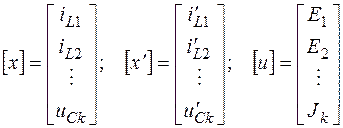

[A] и [B] – матрицы, определяемые структурой цепи и значениями ее параметров.

Аналогично записывают уравнения для выходных величин

[ y ]=[ C ][ x ]+[ D ][ u ], где .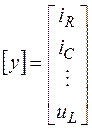

Решения матричных уравнений имеют вид

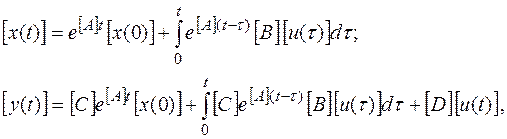
где [ x (0)] – матрица начальных состояний x, e ^{[ A ] t} – переходная матрица состояния системы, называемая иначе фундаментальной.

Для определения фундаментальной матрицы e ^{[ A ] t} существует несколько способов. Однако в последнее время, благодаря широкому использованию вычислительной техники, предпочитают решать систему дифференциальных уравнений численным методом, используя стандартные программы, например MathCAD.

П р и м е р 5.9. Записать уравнения для схемы рис.5.14 методом переменных состояния.

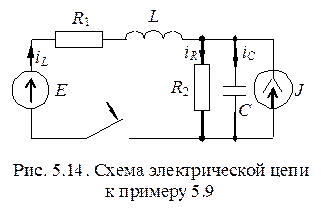Р е ш е н и е.

1. Записываем вначале уравнения по законам Кирхгофа

2. Преобразуем последнее уравнение 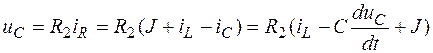и затем предпоследнее уравнение .

3. Переносим производные i¢_L и i¢_C в левую часть уравнений

4. В матричной форме система дифференциальных уравнений имеет вид

или .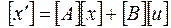

5. Дополняя эту систему начальными условиями i_L (0₊) = 0, u_C (0₊) =JR ₂, можно определять i_L(t), и u_C(t) с помощью программы MathCAD.

6. Если требуется определить другие величины i_R, i_C, u_L, то составим алгебраические уравнения

7. Тогда система алгебраических уравнений имеет вид или .

Дата добавления: 2014-12-27