КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Расчет переходных процессов в разветвленной цепи
|
|
|
|
Расчет целесообразно вести, придерживаясь определенной последовательности:
1) задаем положительные направления токов во всех ветвях и определяем независимые начальные условия uC (0), iL (0);
2) составляем уравнения по законам Кирхгофа для схемы, получившейся после коммутации;
3) определяем корни характеристического уравнения, приравняв нулю входное сопротивление любой ветви схемы, т.е. Z (p) = 0;
4) определяем начальные условия искомых токов или напряжений i (0+), u (0+) и их производных (если характеристическое уравнение имеет второй порядок, то необходимы начальные условия тока и его производной, если третий порядок, то потребуется еще и вторая производная тока), для этого используются составленные в п.2 уравнения и определенные в п.1 независимые начальные условия (при необходимости уравнения могут быть продифференцированы);
5) определяем принужденные составляющие iпр, uпр, выполнив расчет схемы в установившемся режиме известными методами;
6) рассчитываем свободные составляющие искомых переходных величин (iсв, uсв), с учетом характера корней, полученных в п. 3; если корень один, то iсв=Aept, A=i (0+)– iпр (0+); если корня два, то для разных корней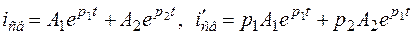 
.
П р и м е р 5.8. Определить переходный ток через конденсатор (рис. 5.13), если E =120 В, R 1= R 3=50 Ом, R 2=10 Ом, L =2 Гн, C =150 мкФ.
Р е ш е н и е. Задаем положительные направления токов и определяем независимые начальные условия
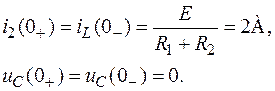
1. Составляем уравнения по законам Кирхгофа для схемы, получившейся после коммутации,
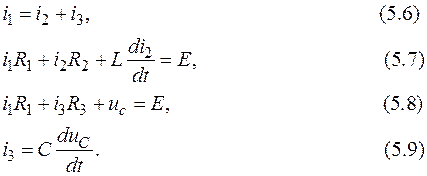
2. Определяем корни характеристического уравнения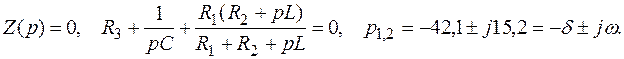 
3. Рассчитываем начальные условия для тока i 3(0+) и его производной i ¢3(0+). Для этого сначала подставим в уравнения (5.6) и (5.8) значения i 2(0+)=2 A и uC (0+)=0. Из получившейся системы уравнений i 1(0+)=2+ i 3(0+) 50 i 1(0+)+50 i 3(0+)+0=120
определяем i 3(0+)=0,2 A, i 1(0+)=2,2 A.
Затем из уравнения (5.7) определим значение производной тока i ¢2(0+):
А/с.
Дифференцируем уравнения (5.6) и (5.8):
i 1¢(0+)= i 2¢(0+)+ i 3¢(0+)= –5+ i 3¢(0+); R 1 i 1¢(0+)+ R 3 i 3¢(0+)+ uC ¢(0+)=0.
Из уравнения (5.9) 
В/с,
тогда 50 i 1¢(0+)+50 i 3¢(0+)+1333=0.
Из этих уравнений получим i 3¢(0+)= –10,8 А/с.
4. Определим принужденную составляющую тока i 3пр. В установившемся режиме ток через конденсатор равен нулю, поэтому i 3пр=0.
5. Определяем свободную составляющую тока i 3св в форме затухающих колебаний 
, так как в п.3 были определены комплексные корни характеристического уравнения. При этом
При t =0+
.
Из этой системы уравнений определим А =0,253, y =127,7.
Таким образом, переходный ток через конденсатор определяется уравнением
.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 1232; Нарушение авторских прав?; Мы поможем в написании вашей работы!