Пример. Анализ эффективности использования производственного потенциала предприятия

Производственные ресурсы	Расход ресурсов за 1 месяц при работе	Общий ресурс
1-м способом	2-м способом
Сырье
Оборудование
Электроэнергия

Предприятие располагает тремя производственными ресурсами (сырьем, оборудованием, электроэнергией) и может организовать производство продукции двумя различными способами. Расход ресурсов за один месяц и общий ресурс при каждом способе производства даны в таблице. При первом способе производства предприятие выпускает за 1 месяц 3 тыс. изделий, при втором – 4 тыс. изделий. Сколько месяцев должно работать предприятие каждым из этих способов, чтобы при наличных ресурсах обеспечить максимальный выпуск продукции?

Решение.

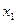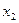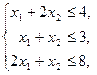
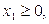
1. Составим математическую модель задачи. Обозначим: - время работы предприятия 1-м способом; - время работы предприятия 2-м способом. max при ограничениях: 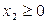. Приведем задачу к каноническому виду: max при ограничениях: .

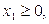
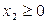2. Составляем симплекс-таблицу 1-го шага:

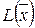
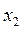
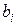
	-3	-4

Получим решение:

.

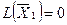В индексной строке есть две отрицательные оценки, значит, найденное решение не является оптимальным и его можно улучшить.

В качестве ключевого столбца следует принять столбец базисной переменной 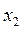, а за ключевую строку взять строку переменной , где 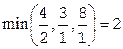. Ключевым элементом является 2. вводим в столбец базисной переменной 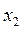, выводим .

3. Составляем симплекс-таблицу 2-го шага:

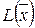
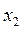
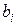
	-1

Получим решение:

.

В индексной строке есть одна отрицательная оценка. Полученное решение можно улучшить. Ключевым элементом является .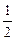

4. Составляем симплекс-таблицу 3-го шага:

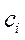
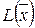
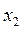
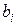
					-1
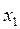
				-1
					-3

Все оценки , следовательно, найденное решение оптимальное.

.

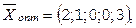
Таким образом, по 1-му способу предприятие должно работать 2 месяца, по 2-му – 1 месяц, при этом максимальный выпуск продукции составит 10 тыс. единиц.

Ответ: 2 месяца, 1 месяц; 10 тыс. ед.

ТЕМА 3. ТРАНСПОРТНАЯ ЗАДАЧА.

Транспортная задача (ТЗ) – одна из распространенных задач линейного программирования. Она возникает при планировании наиболее рациональных перевозок грузов. В одних случаях это означает определение такого плана перевозок, при котором стоимость последних была бы минимальной, в других = более важным является выигрыш во времени.

Первая задача получила название транспортной задачи по критерию стоимости, а вторая – транспортной задачи по критерию времени.

Первая задача является частным случаем ЗЛП и может быть решена симплексным методом. Однако в силу ее особенностей она решается проще.

В общем виде ТЗ можно представить следующим образом:

В m пунктах производства имеется однородный груз в количестве соответственно . Этот груз необходимо доставить в n пунктов назначения в количестве соответственно 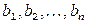. Стоимость перевозки груза (тариф) из пункта в пункт 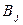равна . Требуется составить план перевозок, позволяющий вывести все грузы и имеющий минимальную стоимость.

В зависимости от соотношения между суммарными запасами груза и суммарными потребностями в нем ТЗ могут быть закрытыми и открытыми.

Если , то ТЗ называется закрытой.

Если 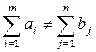, то ТЗ называется открытой.

Обозначим через 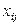количество груза, перевозимого из пункта в пункт 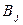. Рассмотрим закрытую ТЗ. Ее условия запишем в распределительную таблицу, которую будем использовать для нахождения решения:

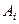
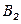
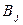
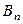
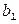
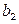
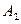
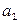
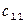
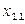
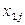
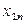
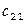
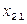
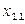
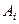
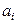
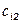
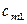
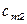
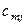
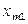
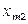
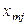
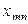
Математическая модель закрытой ТЗ имеет вид: min при ограничениях , , .

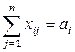Оптимальным решением задачи является матрица , удовлетворяющая системе ограничений и доставляющая минимум целевой функции.

Для решения ТЗ разработан специальный метод, имеющий те же этапы, что и симплексный метод, а именно:

§ нахождение исходного опорного решения;

§ проверка этого решения на оптимальность;

§ переход от одного опорного решения к другому.

Нахождение исходного опорного решения
(ПРАВИЛО «СЕВЕРО-ЗАПАДНОГО УГЛА»)

Заполним распределительную таблицу, начиная с левого верхнего угла, двигаясь далее или по строке вправо, или по столбцу вниз. В клетку (1;1) занесем меньшее из чисел , т.е. .

Если , то 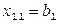и первый столбец «закрыт», т.е. потребности 1-го потребителя удовлетворены полностью. Двигаемся далее по первой строке в соседнюю клетку (1,2), записываем меньшее из чисел , т.е. .

Если , то аналогично «закрывается» 1-ая строка и далее переходим к заполнению соседней клетки (2;1), куда заносим .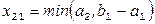

Будем продолжать процесс до тех пор, пока на каком-то этапе не исчерпаются ресурсы 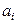и .

Пример. В двух пунктах отправления А и В находится соответственно 150 и 90 т горючего. В пункты 1, 2, 3 требуется доставить соответственно 60, 70 и 110 т горючего. Стоимости перевозок тонны горючего из пункта А в пункты 1, 2, 3 соответственно 6, 10, 4 у.е., а из В – 12, 2, 8 у.е. Составить оптимальный план перевозок горючего так, чтобы общая сумма транспортных расходов была наименьшей.

Дата добавления: 2014-12-27