
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Проверка найденного опорного решения на оптимальность
|
|
|
|
Получив исходно опорное решение, переходят к построению опорных решений, улучшающих друг друга. Для этого применим метод потенциалов по следующему критерию: если опорное решение ТЗ является оптимальным, то ему соответствует система m + n действительных чисел 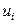 и
и  , удовлетворяющих условиям:
, удовлетворяющих условиям:
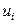 +
+  =
=  - для занятых клеток,
- для занятых клеток,
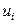 +
+  -
- 
 0 – для свободных клеток.
0 – для свободных клеток.
Числа 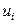 и
и  называются потенциалами. В распределительную таблицу добавляют строку
называются потенциалами. В распределительную таблицу добавляют строку  столбец
столбец 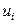 . Потенциалы
. Потенциалы 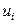 и
и  находят из равенства
находят из равенства 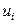 +
+  =
=  , справедливого для занятых клеток. Только одному из потенциалов дается произвольное значение, например
, справедливого для занятых клеток. Только одному из потенциалов дается произвольное значение, например 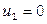 , тогда остальные потенциалы определяются однозначно. Так, если известен потенциал
, тогда остальные потенциалы определяются однозначно. Так, если известен потенциал 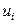 , то
, то  =
=  -
- 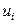 ; если известен потенциал
; если известен потенциал  , то
, то 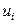 =
=  -
-  .
.
Обозначим 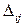 =
= 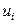 +
+  -
-  . Эту оценку называют оценкой свободных клеток.
. Эту оценку называют оценкой свободных клеток.
Если 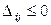 , то опорное решение является оптимальным. Если хотя бы одна из оценок
, то опорное решение является оптимальным. Если хотя бы одна из оценок  , то опорное решение не является оптимальным и его можно улучшить, перейдя от одного опорного решения к другому.
, то опорное решение не является оптимальным и его можно улучшить, перейдя от одного опорного решения к другому.
Наличие положительной оценки свободной клетки  при проверке опорного решения на оптимальность свидетельствует о том, что полученное решение не оптимально и для уменьшения значения целевой функции надо перейти к другому опорному решению. При этом надо перераспределить грузы, перемещая их из занятых клеток в свободные. Свободная клетка становится занятой, а одна из занятых клеток – свободной.
при проверке опорного решения на оптимальность свидетельствует о том, что полученное решение не оптимально и для уменьшения значения целевой функции надо перейти к другому опорному решению. При этом надо перераспределить грузы, перемещая их из занятых клеток в свободные. Свободная клетка становится занятой, а одна из занятых клеток – свободной.
Для свободной клетки с  строится цикл (цепь, многоугольник), все вершины которого, кроме одной, находятся в занятых клетках; углы прямые, число вершин четное. Около свободной клетки цикла ставится знак “+”, затем поочередно проставляют знаки “-” и “+”. У вершин со знаком “-” выбирают минимальный груз; его прибавляют к грузам, стоящим у вершин со знаком “+”, и отнимают от грузов у вершин со знаком “-”.
строится цикл (цепь, многоугольник), все вершины которого, кроме одной, находятся в занятых клетках; углы прямые, число вершин четное. Около свободной клетки цикла ставится знак “+”, затем поочередно проставляют знаки “-” и “+”. У вершин со знаком “-” выбирают минимальный груз; его прибавляют к грузам, стоящим у вершин со знаком “+”, и отнимают от грузов у вершин со знаком “-”.
В результате перераспределения получают новое опорное решение. Это решение проверяют на оптимальность, и т.д. до тех пор, пока не получат оптимальное решение.
Пример.
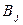
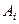
| 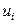
| |||||||
| -2 | ||||||||

|
(1;1): 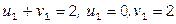 ;
;
(3;1):  ;
;
(3;3):  ;
;
(2;3):  ;
;
(2;2):  ;
;
 =
= 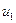 +
+  -
-  ;
;
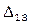 =
= 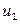 +
+ 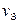 -
-  ;
;
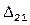 =
= 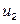 +
+ 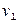 -
- 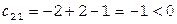 ;
;
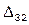 =
= 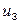 +
+ 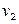 -
- 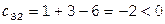 .
.
Опорное решение  не является оптимальным.
не является оптимальным.  у.е. Улучшим его. Строим цикл для клетки (1;3),
у.е. Улучшим его. Строим цикл для клетки (1;3), 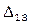
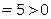 :
:
|
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 404; Нарушение авторских прав?; Мы поможем в написании вашей работы!