Графический метод. Наиболее простым и наглядным методом линейного программирования является графический метод

Наиболее простым и наглядным методом линейного программирования является графический метод. Он применяется для решения ЗЛП с двумя переменными, заданными в неканонической форме и многими переменными, заданными в канонической форме при условии, что они содержат не более двух свободных переменных.

С геометрической точки зрения в ЗЛП ищется такая угловая точка или набор точек из допустимого множества решений, на котором достигается самая верхняя (нижняя) линия уровня, расположенная дальше (ближе) остальных в направлении наискорейшего роста.

Для нахождения экстремального значения целевой функции при графическом решении ЗЛП используют вектор 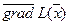на плоскости 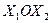, который обозначим 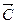. Этот вектор показывает направление наискорейшего изменения целевой функции, он равен 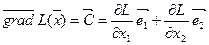, где 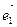, 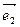- единичные векторы по осям 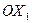и 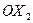соответственно. Таким образом, 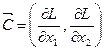. Координатами вектора 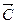являются коэффициенты целевой функции .

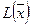Алгоритм решения ЗЛП графическим методом:

1. Находим ОДР системы ограничений ЗЛП.

2. Строим вектор .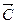

3. Проводим линию уровня 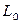, перпендикулярную .

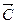4. Линию уровня перемещаем по направлению 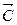для задач на максимум и в направлении, противоположном 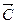, для задач на минимум.

5. Перемещение линии уровня производится до тех пор, пока у нее не окажется одна общая точка с ОДР. Эта точка и будет точкой экстремума.

6. Если окажется, что линия уровня параллельна одной из сторон ОДР, то в таком случае экстремум достигается во всех точках соответствующей стороны, а ЗЛП будет иметь бесконечное множество решений. Говорят, что такая задача имеет альтернативный оптимум.

7. Находим координаты точки экстремума и значение целевой функции в ней.

Исходный продукт	Расход исходных продуктов на 1 кг мороженого	Запас, кг
Сливочное	Шоколадное
Молоко	0,8	0,5
Наполнители	0,4	0,8

Пример. Фирма выпускает два вида мороженого: сливочное и шоколадное. Для изготовления мороженого используются два холодных продукта: молоко и наполнители, расходы которых на 1 кг мороженого и суточные запасы даны в таблице. Изучение рынка сбыта показало, что суточный спрос на сливочное мороженое превышает спрос на шоколадное не более чем на 100 кг. Кроме того, установлено, что спрос на шоколадное мороженое не превышает 350 кг в сутки. Розничная цена 1 кг сливочного мороженого – 16 руб., шоколадного – 14 руб. какое количество мороженого каждого вида должна производить фирма, чтобы доход от реализации продукции был максимальным?

Решение. Обозначим: 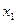- суточный объем выпуска сливочного мороженого, кг; 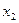- суточный объем выпуска шоколадного мороженого, кг. Составим математическую модель задачи. Целевая функция будет иметь вид: 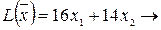max при ограничениях: .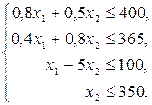

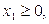
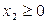§ ОДР – ABCDEF. Строим вектор .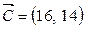

§ Линия уровня 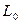задается уравнением 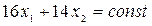. Перемещаем линию по направлению вектора 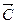. Точкой выхода 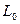из ОДР является точка С – пересечение прямых 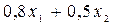=400 и 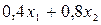=365.

§ С(312,5;300), 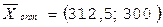, 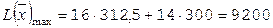р.

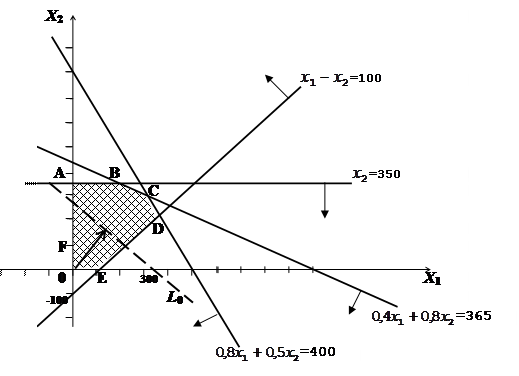
Таким образом, фирма должна выпускать в сутки 312,5 кг сливочного и 300 кг шоколадного мороженого, при этом доход от реализации составит 9200 руб.

Дата добавления: 2014-12-27