
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Исходные данные задачи
|
|
|
|
| Бригада | Производительность бригад, шт/ч | Фонд рабочего времени, ч | |
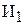
| 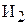
| ||
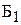
| 9,5 | ||
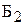
| |||
| Заказ, шт |
Ограничения по заказу изделий имеют следующую содержательную форму записи
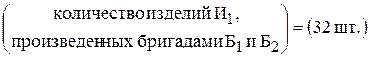
и
 .
.
Математическая форма записи имеет вид
 и
и
 .
.
Ограничение по фондам времени имеет содержательную форму

и
 .
.
Проблема заключается в том, что в условии задачи прямо не задано время, которое тратят бригады на выпуск одного изделия 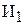 или
или 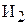 , т.е. не задана трудоемкость производства. Но имеется информация о производительности каждой бригады, т.е. о количестве производимых изделий в 1 ч. Трудоемкость Тр и производительность Пр являются обратными величинами, т.е.
, т.е. не задана трудоемкость производства. Но имеется информация о производительности каждой бригады, т.е. о количестве производимых изделий в 1 ч. Трудоемкость Тр и производительность Пр являются обратными величинами, т.е.
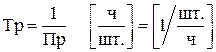 .
.
Поэтому используя табл., получаем следующую информацию:
®  ч тратит бригада
ч тратит бригада 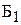 на производство одного изделия
на производство одного изделия 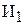 ;
;
®  ч тратит бригада
ч тратит бригада 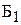 на производство одного изделия
на производство одного изделия  ;
;
®  ч тратит бригада
ч тратит бригада  на производство одного изделия
на производство одного изделия 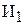 ;
;
® 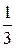 ч тратит бригада
ч тратит бригада  на производство одного изделия
на производство одного изделия  .
.
Запишем ограничения по фондам времени в математическом виде

и
 .
.
Неотрицательность объемов производства задается как
 .
.
Таким образом, математическая модель этой задачи имеет вид
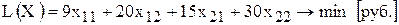 ,
,

Пример. Для пошива одного изделия требуется выкроить из ткани 6 деталей. На швейной фабрике были разработаны два варианта раскроя ткани. В табл.1.3 приведены характеристики вариантов раскроя 10  ткани и комплектность, т.е. количество деталей определенного вида, которые необходимы для пошива одного изделия. Ежемесячный запас ткани для пошива изделий данного типа составляет 405
ткани и комплектность, т.е. количество деталей определенного вида, которые необходимы для пошива одного изделия. Ежемесячный запас ткани для пошива изделий данного типа составляет 405  . В ближайший месяц планируется сшить 90 изделий.
. В ближайший месяц планируется сшить 90 изделий.
Постройте математическую модель задачи, позволяющую в ближайший месяц выполнить план по пошиву с минимальным количеством отходов.
Характеристики вариантов раскроя отрезов ткани по 10 
| Вариант раскроя | Количество деталей, шт./отрез | Отходы,  /отрез /отрез
| |||||
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| 0,5 | |||||||
| 0,35 | |||||||
| Комплектность, шт./изделие |
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 549; Нарушение авторских прав?; Мы поможем в написании вашей работы!