
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Понятие о дифференциальном уравнении
|
|
|
|
Дифференциальные уравнения
4.1 Методические указания по теме «Дифференциальные уравнения»
Дифференциальным уравнением называется уравнение, связывающее независимую переменную, искомую функцию, ее производную (или дифференциал аргумента и дифференциал функции).
Если дифференциальное уравнение содержит производную или дифференциал не выше первого порядка, то оно называется дифференциальным уравнением первого порядка. Общий вид такого уравнения 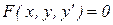 , где
, где 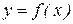 – искомая неизвестная функция
– искомая неизвестная функция  – ее производная по
– ее производная по  , а
, а  – заданная функция переменных
– заданная функция переменных  .
.
Общим решением дифференциального уравнения первого порядка называется функция  от
от 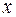 и произвольной постоянной
и произвольной постоянной 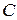 , обращающая это уравнение в тождество по
, обращающая это уравнение в тождество по 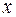 .
.
Общее решение, записанное в неявном виде 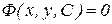 , называется общим интегралом.
, называется общим интегралом.
Частным решением уравнения 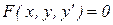 называется решение, полученное из общего решения при фиксированном значении
называется решение, полученное из общего решения при фиксированном значении  , где
, где  – фиксированное число.
– фиксированное число.
Частным интегралом уравнения 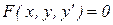 называется интеграл, полученный из общего интеграла при фиксированном значении
называется интеграл, полученный из общего интеграла при фиксированном значении  .
.
График любого частного решения дифференциального уравнения 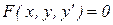 называется интегральной кривой. Общему решению (и общему интегралу) этого уравнения соответствует семейство интегральных кривых, зависящих от одного параметра.
называется интегральной кривой. Общему решению (и общему интегралу) этого уравнения соответствует семейство интегральных кривых, зависящих от одного параметра.
Задача нахождения частного интеграла дифференциального уравнения 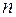 - го порядка
- го порядка 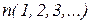 , удовлетворяющего начальным условиям вида
, удовлетворяющего начальным условиям вида 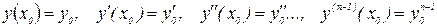 , называется задачей Коши.
, называется задачей Коши.
Задача Коши для дифференциального уравнения первого порядка состоит в том, чтобы найти решение, удовлетворяющее начальному условию  . Другими словами, из всех интегральных кривых данного дифференциального уравнения требуется выделить ту, которая проходит через данную точку
. Другими словами, из всех интегральных кривых данного дифференциального уравнения требуется выделить ту, которая проходит через данную точку 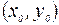 .
.
Дифференциальные уравнения с разделяющимися переменными Общий вид такого уравнения:
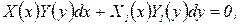 где
где 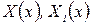 – функции только от
– функции только от  – функции только от
– функции только от 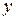 .
.
Поделив обе части уравнения на произведение  , получим уравнение с разделёнными переменными:
, получим уравнение с разделёнными переменными:
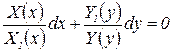 .
.
Общий интеграл этого уравнения имеет вид:
 .
.
З а м е ч а н и е. Если произведение  при
при  и
и 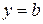 , то эти функции
, то эти функции  и
и 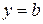 являются решениями дифференциального уравнения при условии, что при этих значениях
являются решениями дифференциального уравнения при условии, что при этих значениях 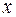 и
и 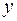 уравнение не теряет числового смысла. Геометрически эти решения представляют собой прямые, параллельные осям координат.
уравнение не теряет числового смысла. Геометрически эти решения представляют собой прямые, параллельные осям координат.
Пример 1. Решить уравнение 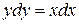 . Найти частное решение, удовлетворяющее условию
. Найти частное решение, удовлетворяющее условию  при
при 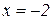 .
.
Р е ш е н и е. Это уравнение с разделёнными переменными. Интегрируя, находим общее решение уравнения:
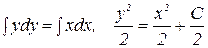 .
.
Для получения более простого по форме общего решения постоянное слагаемое в правой части представлено в виде  . Тогда
. Тогда  .
.
Подставив в общее решение значения  и
и 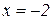 , получим
, получим 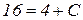 , откуда
, откуда 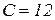 .
.
Итак, частное решение уравнения, удовлетворяющие данному условию, имеет вид 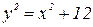 .
.
Пример 2. Найти общий интеграл дифференциального уравнения  .
.
Р е ш е н и е. Так как 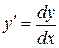 , то
, то  , откуда
, откуда  .
.
Разделим обе части уравнения на произведение 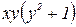 :
:
 .
.
Преобразуем дробь:
 .
.
Тогда:
 .
.
Интегрируя, находим:
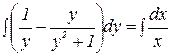 ,
, 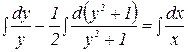 ,
,
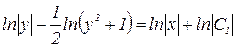 ,
, 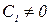 .
.
Для облегчения потенцирования и получения более простого по форме общего решения постоянное слагаемое в правой части представлено в виде  . После потенцирования получим:
. После потенцирования получим:
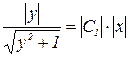 откуда
откуда 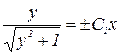 , или
, или  , где
, где 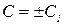 .
.
Произведение 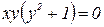 при
при 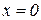 и при
и при 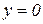 . При этих значениях
. При этих значениях  и
и 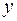 дифференциальное уравнение не теряет числового смысла, поэтому
дифференциальное уравнение не теряет числового смысла, поэтому  и
и 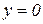 – решение уравнения, но решение
– решение уравнения, но решение  входит в решение
входит в решение 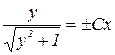 при
при 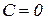 .
.
Значит, решения уравнения имеют вид  и
и 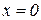 .
.
Пример 3. Решить уравнение:
 . Найти частное решение, удовлетворяющие условию
. Найти частное решение, удовлетворяющие условию  при
при 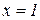 .
.
Р е ш е н и е. Разделим каждый член уравнения на произведение:
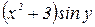 :
:  .
.
Интегрируя, находим:
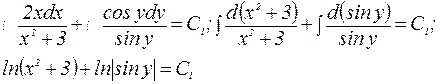
После потенцирования получим: 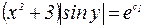 ,
, 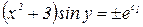 или
или 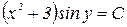 , где
, где 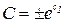 . Отсюда
. Отсюда  .
.
Произведение 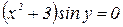 при
при  ; так как при этом значении дифференциальное уравнение не теряет числового смысла, то
; так как при этом значении дифференциальное уравнение не теряет числового смысла, то  – решение уравнения. Но оно входит в интеграл
– решение уравнения. Но оно входит в интеграл 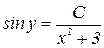 при
при 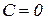 .
.
Значит, общий интеграл уравнения имеет вид: 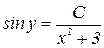 .
.
Подставив в общий интеграл значения  и
и 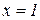 , получим
, получим  , откуда
, откуда 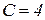 . Итак, частный интеграл уравнения, удовлетворяющий данному условию, имеет вид:
. Итак, частный интеграл уравнения, удовлетворяющий данному условию, имеет вид:  .
.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 582; Нарушение авторских прав?; Мы поможем в написании вашей работы!