Размещения

Основные понятия комбинаторики

Теория вероятностей

5.1 Методические указания по теме «Теория вероятностей»

Задачи, при решении которых приходится составлять различные комбинации из конечного числа элементов и производить подсчет числа всех возможных таких комбинаций, называются комбинаторными.

Раздел математики «Теория вероятностей» находит широкое практическое применение во многих вопросах естествознания и техники.

Пусть имеется множество, содержащее n элементов. Каждое его упорядоченное подмножество, содержащее по m элементов, называется размещением из n элементов по m элементов.

Из определения вытекает, что 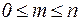и что размещения из n элементов по m – это все m-элементарные подмножества, отличающиеся составом элементов или порядком их следования.

Число размещений из n элементов по m элементов в каждом обозначают 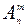и вычисляют по формуле: .

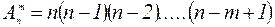Число размещений из n элементов по m элементов в каждом равно произведению m последовательно убывающих натуральных чисел, из которых большее есть n.

Для краткости произведение первых n натуральных чисел принято обозначать n! (n-факториал):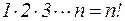

Условились считать, что 0!=1.

Тогда формулу числа размещений из n элементов по m элементов можно записать в другом виде:

.

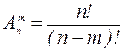Условились считать, что .

Пример 1. Сколькими способами из группы, включающей 25 учащихся, можно выбрать актив группы в составе старосты, комсорга и профорга?

Р е ш е н и е. Состав актива группы является упорядоченным множеством из 25 элементов по 3 элемента. Значит, искомое число способов равно числу размещений из 25 элементов по 3 элемента в каждом:

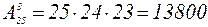
или .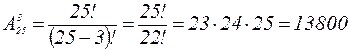

Пример 2. Перед выпуском группа учащихся в 30 человек обменялась фотокарточками. Сколько всего было роздано фотокарточек?

Р е ш е н и е. Передача фотокарточки одним учащимся другому есть размещение из 30 элементов по 2 элемента. Искомое число фотокарточек равно числу размещений из 30 элементов по 2 элемента в каждом:

.

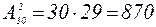Дата добавления: 2014-12-27