Процесс дисконтирования. Функция настоящей стоимости единицы

Процесс дисконтирования обратен процессу наращения. Примером дисконтирования по схеме простых процентов является уже известный нам учет векселей. В общем случае, математика дисконтирования по простой процентной ставке приведена в табл. 2.2.

Табл. 2.2

Вывод формулы дисконтирующего множителя для схемы простых процентов

Момент времени t	Сумма, накопленная к моменту t (FV)
T	PV = FV
T-1	PV = FV - FV´r = FV´(1-r)
T-2	PV = FV - FV´r - FV´r = FV´(1-2r)
T-3	PV = FV - FV´r - FV´r - FV´r = FV´(1-3r)
…
	PV = FV´(1-T´r)

Т – время до момента поступления суммы FV.

– дисконтирующий множитель в условиях действия схемы простых процентов.

В случае действия схемы сложных процентов, по аналогии с процессом наращения, нам придется не умножать, а делить FV на (1+ r).

Табл. 2.3

Вывод формулы дисконтирующего множителя для схемы сложных процентов

Момент времени t	Сумма, накопленная к моменту t (FV)
	PV = FV
	FV=PV´(1+r)
	FV=PV´(1+r)^2
	FV=PV´(1+r)^3
…
T	FV=PV´(1+r)^T

– дисконтирующий множитель для схемы сложных процентов или коэффициент дисконтирования. Множитель показывает, во сколько раз уменьшится ценность суммы FV за t периодов при ставке r. Это вторая стандартная функция сложного процента, также называемая настоящая стоимость единицы. Если сумма, ожидаемая к поступлению через t периодов при ставке r, равна 1, дисконтированная, приведенная ее ценность составит . Во втором приложении к пособию приводятся табулированные значения этой стандартной функции сложного процента.

Графически процесс дисконтирования по сложной процентной ставке иллюстрируется диаграммой на рис. 8.

Рис. 8 Дисконтирование по сложной процентной ставке

Задача 51

У Вас есть возможность выбора между получением 5000 долл. через год или 12000 долл. через 6 лет. Каков Ваш выбор, если ставка доходности составляет: а) 12%; б) 20%?

При ставке 12%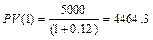

Следует выбрать второй вариант.

При ставке 20%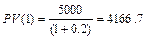

Следует выбрать первый вариант.

Дата добавления: 2014-12-27