Взнос на амортизацию единицы и коэффициент фонда возмещения

При оценке аннуитетов правомочна постановка обратной задачи: определить величину разового взноса при известной настоящей либо будущей стоимости. Исходя из материалов разделов 3.2 и 3.3,

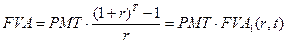(формула 3.3)

(формула 3.7)

Следовательно, величины взносов (PMT) определяются по формулам:

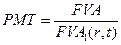для потока с известной будущей (накопленной) стоимостью;

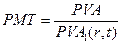для потока с известной настоящей (приведенной) стоимостью.

Величины, обратные FVA₁ и PVA₁, представляют собой пятую и шестую стандартные функции сложного процента и имеют собственные названия и экономическую интерпретацию:

(3.14)

SFF – коэффициент фонда возмещения (Sinking Fund Factor) – величина разового платежа, аннуитетный ряд из которых продолжительностью T даст при ставке r будущую стоимость потока, равную единице.

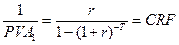(3.15)

CRF – взнос на амортизацию единицы или коэффициент покрытия (Capital Recovery Factor или Capital Recovery and Loan Amortisation) – величина разовой выплаты, аннуитетный ряд из которых за T периодов при ставке r полностью покроют фонд размером в единицу.

Задача 67

Чему должен быть равен ежемесячный вклад по условиям задачи №61, чтобы накопленной суммы хватило?

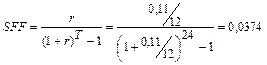
Задача 68

Вам предлагают ежегодно на протяжении 10 лет делать взнос в размере 3000 долл. с целью потом, также на протяжении 10 лет, получать из накопленного фонда содержание (на оба варианта выплат действует схема постнумерандо). Определите размер ежегодного содержания, если по взносам начисляется 15% годовых с ежегодным начислением.

Определяем величину фонда:

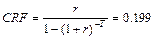
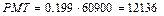долл.

Задача 69

Вам необходимо накопить 25 тыс. долл. за 8 лет. Каким должен быть ежегодный взнос в банк (схема пренумерандо), если банк предлагает 10% годовых? Какую сумму нужно было бы единовременно положить в банк сегодня, чтобы достичь той же цели?

Нужно рассчитать функцию коэффициента фонда возмещения, а затем не забыть что аннуитет пренумерандо.

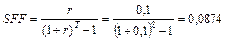- стандартная функция коэффициента фонда возмещения.

Будущая стоимость потока пренумерандо 25 тыс. Для потока постнумерандо:

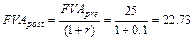
Величина взноса 22,73*0,0874=1,9874 тыс. долл.=1987,4 долл.

Ищем размер единовременного вклада:

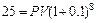
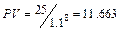тыс. долл.

3.5. Оценка аннуитетов с несовпадающими периодами взносов и начислений процента*

Несовпадение частоты взносов (выплат) и начислений процентов – довольно частое явление при реализации различных накопительных и амортизирующих схем. При этом, игнорирование структурной сущности потока в такой ситуации может привести к результатам расчетов, противоречащим природе финансовых вычислений, в чем нам предстоит убедиться на конкретных примерах. На грубые ошибки всегда укажет и решение задачи «прямым счетом». Поэтому в каждой конкретной ситуации следует сначала убедиться, что периоды взносов и начислений совпадают, а затем применять к ним рассмотренные ранее методы решения и стандартные финансовые функции.

Если частоты не совпадают, можно столкнуться с двумя ситуациями:

1. Частота взносов меньше частоты начисления процентов (взносы либо выплаты осуществляются реже периода капитализации);

2. Поступления (выплаты) осуществляются чаще, чем финансовое учреждение начисляет проценты на них.

Методики расчетов для этих двух ситуаций различны, поэтому их целесообразно рассмотреть подробнее

Дата добавления: 2014-12-27