Аннуитеты с частотой платежей меньше периода начисления процента

В данной ситуации начисление процентов на величину каждого взноса осуществляется несколько раз. Поэтому к концу каждого периода взноса на счете образуется сумма, равная

, где

m – количество начислений в рамках периода взносов (выплат);

r – номинальная процентная ставка, соответствующая периоду начисления (месячная, квартальная и т.п.).

Оценка такого аннуитета сводится к вычислению финансово эквивалентной ставки , соответствующей периоду осуществления взносов. Не сложно заметить, что если период аннуитета равен 1 году, это эффективная процентная ставка. В этом отношении, эффективные ставки являются разновидностью эквивалентных.

Далее аннуитет можно оценивать по стандартным рассмотренным ранее методикам, применив в расчетах пересчитанное значение процентной ставки.

Аннуитеты пренумерандо можно преобразовывать к потокам постнумерандо путем расчета суммы, образующейся на счете к концу каждого периода и далее заменять в формулах и ставку на эквивалентную, и величину взноса на полученную в ходе приведения к концу периода.

Задача 70*

Вы имеете возможность в течение 5 лет вносить в банк каждые полгода по 1000 долл. по схеме пренумерандо. Банк начисляет 12% годовых: а) раз в полгода; б) ежеквартально; в) ежемесячно. Какая сумма будет на счете в конце срока?

а) аннуитет пренумерандо с совпадающей частотой взносов и начислений процента.

б) взносы реже начислений, m = 2, r = 3%.

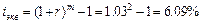
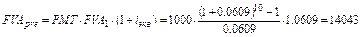или

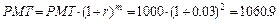
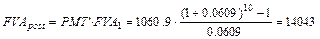
в) взносы реже начислений, m = 6, r = 1%.

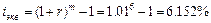
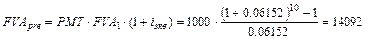
Задача 71*

На протяжении 3-х лет Вы получали от родителей по 4000 в год (в начале). Какая сумма накопится на вашем счете к концу третьего года? Сколько нужно было бы вносить ежемесячно, чтобы сумма, накопленная за те же три года, была равна 20000 (15% годовых сложных, ежемесячное начисление).

Первый вариант – аннуитет пренумерандо. Поскольку начисление процентов ежемесячное, необходимо преобразовать его к аннуитету постнумерандо, рассчитав будущие стоимости взносов размером по 4 тыс. к концу года при ежемесячном начислении.

PMT'=4000*(1+0.15/12)¹²=4643

Затем ищем эффективную ставку, соответствующую 15% сложных при ежемесячном начислении:

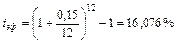
Теперь можно рассчитать будущую стоимость аннуитета с размером взноса 4643, осуществляемым ежегодно при годовой ставке 16,076%. Аннуитет идет 3 года.

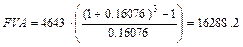
Для определения ежемесячного взноса при известной накопленной сумме в 20000 используем стандартную функцию коэффициента фонда возмещения.

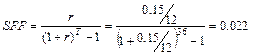
Размер взноса

Дата добавления: 2014-12-27