Методические указания. Работа № 7. Многомерные методы оптимизации

Работа № 7. Многомерные методы оптимизации

Задание

1. Ознакомиться с методами многомерной оптимизации: методом Хука-Дживса, методом покоординатного спуска, методом наискорейшего спуска и методом градиента.

2. Составить программу расчета для одного из методов, согласно варианту задания, по двум параметрам для задачи без ограничения и отладить ее на контрольном примере.

3. Решить задачу оптимизации для целевой функции и параметров, согласно данным варианта.

1. Постановка задачи нелинейного программирования и многомерные методы приведены в разделе 3, тема 5. В данной работе многомерная оптимизация рассматривается на примере двухпараметрической задачи. В качестве методов использованы, в зависимости от варианта, метод Хука-Дживса и метод покоординатного спуска, которые относятся к методам нулевого порядка.

Алгоритм любого из методов поисковой многомерной оптимизации состоит из двух этапов:

1) Определение направления движения в пространстве параметров на текущем шаге.

2) Движение вдоль выбранного направления одним из методов одномерной оптимизации.

На первом этапе в обоих из названных методов направление выбирается вдоль координаты.

На втором – в задаче без ограничений – целесообразно использовать одномерный метод равномерного поиска, как в методе Хука-Дживса, так и в методе покоординатного спуска (см. работа №1), который рекомендуется модифицировать, введя переменный шаг (при удачном продвижении величина шага удваивается, при неудачном – делится пополам).

Процесс оптимизации завершается, когда удовлетворяется заданная точность одновременно по обеим координатам.

2. При составлении программы многомерного метода рекомендуется воспользоваться готовой программой одномерного метода равномерного поиска, использованной в работе №1. Эта программа выполняет роль внутренней процедуры и дополняется модулем чередования координат, из которого к ней производится обращение.

В качестве параметров оптимизации принимаются переменные х и у, область допустимых значений параметров определена границами (Ах,Вх и Ау,Ву),точность по каждому параметру соответственно Ех и Еу. Выражение целевой функции записывается в виде: Z(x,y)=F(x) +H(y).

Для определения координат текущей точки в области параметров оптимизации рекомендуется использовать двумерные массивы Mathcad.

Текст программы формирования целевой функции Z(x,y), а также ее геометрическая интерпретация для отладочного примера в 3D и 2D графиках приведен на рис. 36. Вызов процедур вMathCad производится согласно инструкции по работе вMathCad (см. раздел 4).

Программа двумерной оптимизации методом покоординатного спуска в MathCad и результаты оптимизационного расчета для отладочного примера приведены на рис. 37. Использованы вспомогательные машинные переменные для аргумента t и целевой функции Р(Х,Y), а также рабочие ячейки G и H. Одномерный метод равномерного поиска оформлен в виде процедуры и обозначен в программе L(P, a, e), где параметры P, a, e формальные параметры процедуры которым при обращении присваиваются фактические значения. Результаты расчетов: координаты точки минимума обозначены идентификаторами (Xm,Ym), а значение целевой функции в этой точке − Z(Xm,Ym).

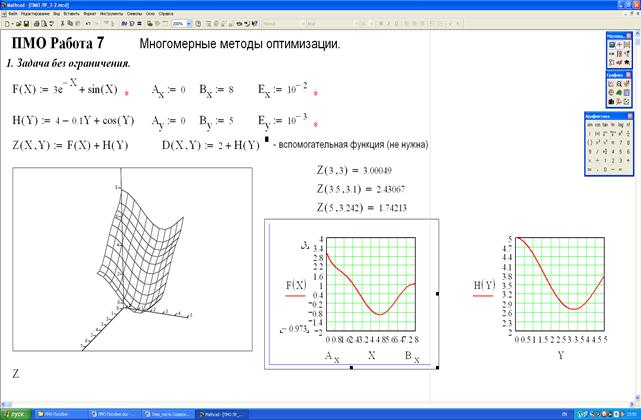
Рис.36. Программа построения целевой функции от двух параметров в Mathcad.

Рис. 37. Программа двумерной оптимизации в MathCad.

3. При выполнении оптимизации согласно варианту для целевой функции и параметров, используются данные, представленные в табл. 7. Варианты заданий, как по методу, так и по компонентам F(x) и H(y) целевой функции Z(x,y), а также интервалам по координатам х и у отражены сочетанием номеров строк табл. 7. Компоненты целевой функции F(x) и H(y), значения границ интервалов – (Ах,Вх) и (Ау,Ву), а такжезначения точностей Ех и Еу по каждой из кооринат – х и у берутся из графы «номер функции» табл.7. В качестве стартовой принимается точка С(Ах,Ау) на границе области допустимых значений параметров оптимизации (Ах,Вх и Ау,Ву).

Таблица 7. Варианты заданий.

№ варианта

Метод

Хука-Дживса

Поокординатного спуска

Номер F(x)

Номер H(y)

Номер функции

Целевая функция Z(x,y) =F (x) + H(y)

Интервал (а,b)

Точность e

4 – 0,1 х + cos(x)

0 – 5,0

0,1

х ² + 1/ х

0,1 – 2,0

0,01

tg(x) + 1/ х

0,1 – 1,5

0,001

exp(x) + 1/ х

0,1 – 1,0

0,01

tg(x) – ln(x)

0,1 – 1,0

0,001

3۰exp(– x) + sin(x)

0 – 8,0

0,1

В программе двумерной оптимизации по методу Хука-Дживса используется дополнительный цикл, который обеспечивает чередование смены направлений движения к точке минимума на каждом цикле расчета.

Работа № 8. Многомерная оптимизация при ограничениях

Задание

1. Ознакомиться с методами многомерной оптимизации при ограничениях: методом движения вдоль границ, отражения от границ.

2. Составить программу расчета для одного из методов, согласно варианту задания по двум параметрам для задачи с ограничениями и отладить ее на контрольном примере.

3. Решить задачу оптимизации с ограничениями для целевой функции и параметров согласно данным варианта.

Дата добавления: 2014-12-27