Первообразная и неопределенный интеграл

Неопределенный интеграл

Теоретические вопросы

Введение

ВЫСШАЯ МАТЕМАТИКА

Контрольные задания и методические указания

для студентов заочного отделения

инженерно-технических специальностей

(вторая часть)

ВЕЛИКИЙ НОВГОРОД

Р е ц е н з е н т

В.А. Едемский

Высшая математика: Контрольные задания и метод. указания для студентов заочного отделения инженерно-технических специальностей (вторая часть) / Сост. С.О. Карданов, Е.Ю. Карданова; НовГУ им. Ярослава Мудрого. – Великий Новгород, 2006. – 46с.

Пособие является руководством по выполнению контрольных работ по курсу высшей математики дл студентов-заочников инженерно-технических специальностей вузов. Оно содержит вопросы и теоретические сведения, необходимые для выполнения контрольных работ по данной теме, примеры решения задач, контрольные задания и список литературы.

При изучении курса высшей математики студент-заочник должен выполнить ряд контрольных работ. Решения задач и пояснения к ним должны быть достаточно подробными. Все решения надо приводить полностью, чертежи и графики должны быть выполнены четко, с указанием масштаба и названий координатных осей. Обозначения к задачам должны соответствовать указаниям на чертежах и графиках. К выполнению контрольного задания следует приступать после изучения теоретического материала по учебникам и решения достаточного количества задач по материалу, соответствующему этому заданию. Данное пособие предназначено для студентов-заочников 1-го курса весеннего семестра.

Глава I. Неопределенные и определенные интегралы

1. Первообразная функции.

2. Неопределенный интеграл и его свойства.

3. Таблица основных интегралов.

4. Методы интегрирования.

5. Интегрирование рациональных функций.

6. Интегрирование тригонометрических функций.

7. Интегрирование иррациональных функций.

8. Определенный интеграл и его свойства.

9. Формула Ньютона-Лейбница.

10. Методы вычисления определенных интегралов.

11. Несобственные интегралы.

12. Приложения определенных интегралов.

Литература

1. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. М.: Наука, 1989. Т.1,2.

2. Щипачев В.С. Высшая математика. М.: Высш. шк., 1990.

3. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. М.: Высш. шк.,1998. Ч.1,2.

Функция 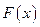называется первообразной функции 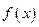на промежутке 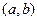, если .

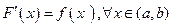Если функция 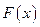- первообразная функции 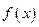на промежутке 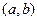, то и функция 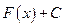, где , тоже является первообразной функции 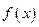на промежутке 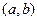. Любые две первообразные и функции 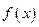связаны соотношением: .

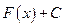
Совокупность всех первообразных функции 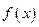называется неопределенным интегралом от функции 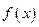и обозначается 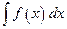. Таким образом, по определению .

Свойство линейности неопределенного интеграла

1.

2.

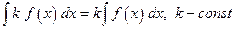
Таблица неопределенных интегралов

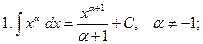
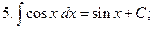
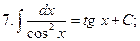
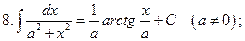
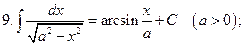
При решении задач могут быть полезны формулы:

1. ;

2. ;

3. .

Дата добавления: 2014-12-27