
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Закон сохранения момента импульса
|
|
|
|
Закон сохранения количества движения (импульса тела).
Импульсом тела (количеством движения) называется векторная величина  равная произведению массы тела m на его скорость
равная произведению массы тела m на его скорость 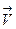 :
:
 = m
= m 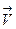 . (19)
. (19)
В изолированной системе суммарный импульс составляющих её тел сохраняется при любых процессах, происходящих в этой сиcтеме:
 =
=  = const, (20)
= const, (20)
где:  - импульс системы;
- импульс системы; 

 - импульсы отдельных тел (частей), составляющих систему.
- импульсы отдельных тел (частей), составляющих систему.
Это и есть закон сохранения импульса.
Импульсы отдельных частей (тел) изолированной системы могут изменяться, но для системы в целом верно выражение (20).
В том случае, когда на систему действуют внешние силы (открытая система), ее количество движения может изменяться. При этом:
 (21)
(21)
где: m – масса системы тел,  - изменение скорости системы как целого;
- изменение скорости системы как целого; 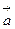 - ускорение, получаемое системой в целом;
- ускорение, получаемое системой в целом;  - время действия внешних сил;
- время действия внешних сил; 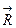 - результирующая внешних сил; i - любое целое число.
- результирующая внешних сил; i - любое целое число.
Произведение  называют импульсом силы. Учитывая это можно сказать, что изменение импульса системы тел равно импульсу действующей на систему внешней силы.
называют импульсом силы. Учитывая это можно сказать, что изменение импульса системы тел равно импульсу действующей на систему внешней силы.
Понятно, что чем больше значение силы 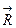 и дольше время ее действия, тем сильнее изменяется количество движения системы.
и дольше время ее действия, тем сильнее изменяется количество движения системы.
В качестве абстрактного примера рассмотрим коробок массой m, покоящийся на поверхности, по которой может перемещаться без трения (рис.6). Внутри этого коробка может практически без трения перекатываться шарик, масса которого m ш сравнима с массой коробка. Коробок и шарик неподвижны в некоторой системе отсчета, т.е. их суммарное количество движения равно нулю:
 ш
ш 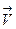 ш0 +
ш0 +  к
к 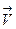 к0 = 0, (22)
к0 = 0, (22)
где: m ши m к – масса шарика и коробка; Vш0иVк0 – начальные скорости шарика и коробка, соответственно.

Рис. 6. Иллюстрация закона сохранения импульса тела
Если шарик начнет перемещаться по коробку, то будет
 ш
ш 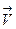 ш ¹ 0. (23)
ш ¹ 0. (23)
Но по закону сохранения импульса, импульс системы коробок - шарик останется равным нулю
 к
к 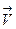 к +
к +  ш
ш 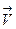 ш = 0,
ш = 0,
или
 к
к 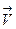 к = -
к = -  ш
ш 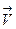 ш ¹ 0, (24)
ш ¹ 0, (24)
где: 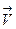 к и
к и 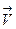 ш – скорости коробка и шарика.
ш – скорости коробка и шарика.
Коробок получит импульс 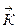 к, равный и противоположный по направлению импульсу
к, равный и противоположный по направлению импульсу 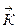 ш.
ш.
Близким к рассмотренному реальным примером может быть следующий. По легкой неподвижной лодке, находящейся в спокойной воде, человек переходит с носа на корму. Лодка при этом переходит в движение в противоположном направлении.
Примерами попыток пренебречь законом сохранения импульса тела служат эпизоды из «правдивых» воспоминаний барона Мюнхгаузена: выдергивание за косичку самого себя и своего коня из болота и ускорение движения корабля, на котором барон находился, надуванием парусов этого же корабля.
Самым ярким и практически широко используемым применением закона сохранения количества движения является, несомненно, реактивное движение (ракеты, самолеты, суда с водомётным двигателем и т.д., а также живые «водомёты» – осьминоги, медузы и проч.).
Если некоторое тело имеет ось вращения, то к нему применимо понятие момента импульса.
Моментом импульса тела (моментом количества движения)  называется величина, равная векторному произведению радиуса-вектора
называется величина, равная векторному произведению радиуса-вектора  на импульс
на импульс  .
.
Закон сохранения момента импульса читается следующим образом: если на тело (систему тел) не действуют никакие внешние силы (изолированная система), то момент импульса этой системы не изменяется:
 =
=  ×
×  =
=  ×
×  = cоnst. (25)
= cоnst. (25)
Заменяя линейную скорость вращения тела на угловую по формуле:
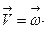
 , получаем:
, получаем:
 =
= 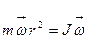 , (26)
, (26)
где J =  - момент инерции тела (материальной точки).
- момент инерции тела (материальной точки).
Из выражения (25) следует, что при уменьшении радиуса вращающегося тела скорость его вращения, в силу того, что  = const, должна увеличиваться. Этот эффект используют, например, фигуристы на льду, когда начинают раскручивание (особенно в финале выступления) с раскинутыми руками, а затем резко прижимают их к телу.
= const, должна увеличиваться. Этот эффект используют, например, фигуристы на льду, когда начинают раскручивание (особенно в финале выступления) с раскинутыми руками, а затем резко прижимают их к телу.
Наличие у вертолетов кроме основного, несущего винта, дополнительного, также связано с законом сохранения момента количества движения.
На законе сохранения момента количества движения основано поведение так называемых гироскопических систем. Гироскопом (волчком) называют применяемые в технике массивные симметричные тела, вращающиеся с большой угловой скоростью.
Гироскопический эффект применяется в нарезных орудиях, гироскопических компасах и других навигационных приборах («искусственный горизонт»). За счет гироскопического эффекта сохраняют стабильное положение в пространстве велосипеды с вращающимися колесами и космические объекты (Земля и другие планеты, звезды и прочее).
Гироскопический эффект учитывается при конструировании турбин и других быстро вращающихся механизмов на транспортных средствах (например, кораблях).
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 580; Нарушение авторских прав?; Мы поможем в написании вашей работы!