
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Типовые математические схемы моделей систем
|
|
|
|
3.1 Динамические системы. Дифференциальные и разностные уравнения
3 .1.1 Системы обыкновенных дифференциальных уравнений
Этот класс моделей хорошо описывает поведение реальных детерминированных и стохастических систем с непрерывным состоянием и непрерывным временем переходов, если неизвестные переменные состояния являются функциями одной независимой переменной – времени. Если независимых переменных больше одной, то используется модель в классе уравнений в частных производных. Ими описываются многие физические процессы и явления, развивающиеся во времени ( -схемы).
-схемы).
В общем, виде можно записать:
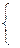
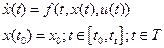 – уравнение состояния, (1)
– уравнение состояния, (1)
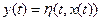 – уравнение выхода. (2)
– уравнение выхода. (2)
Частным видом таких уравнений являются системы линейных дифференциальных уравнений. Если функции f и 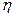 являются линейными функциями x и u, то система и модель называются линейными непрерывными. В противном случае – нелинейными непрерывными.
являются линейными функциями x и u, то система и модель называются линейными непрерывными. В противном случае – нелинейными непрерывными.
Линейная модель имеет вид:
 – уравнения состояния, (3)
– уравнения состояния, (3)
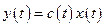 – уравнение выхода, (4)
– уравнение выхода, (4)
 –
– 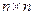 собственная матрица системы,
собственная матрица системы,
 –
– 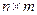 матрица входа,
матрица входа,
 –
– 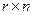 матрица выхода,
матрица выхода,
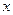 –
–  вектор состояния,
вектор состояния,
 –
– 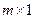 вектор входа,
вектор входа,
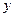 – r
– r 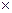 1 вектор выхода.
1 вектор выхода.
Если f и 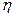 не зависят явно от переменной
не зависят явно от переменной 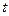 , то систему (модель) называют стационарной, в противном случае – нестационарной.
, то систему (модель) называют стационарной, в противном случае – нестационарной.
Для линейных систем (моделей) переходная функция состояния выражается формулой Коши, представляющей решение системы уравнений (3) в виде:
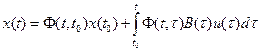 . (5)
. (5)
В теории управления первый член правой части (5) определяют как свободную составляющую вектора состояния, а второй – как вынужденную. Тогда получим:
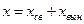 ,
,
где:
 – общее решение однородной системы
– общее решение однородной системы
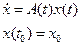 ,
,
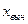 – частное решение неоднородной системы (3),
– частное решение неоднородной системы (3),
 – переходная матрица состояний.
– переходная матрица состояний.
Выражение  определяет импульсную переходную матрицу.
определяет импульсную переходную матрицу.
Физический смысл элементов 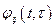 матрицы переходной функции состояния
матрицы переходной функции состояния  следует из первого слагаемого в (5). Это реакция в момент
следует из первого слагаемого в (5). Это реакция в момент 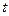 по
по  – ой составляющей вектора состояний
– ой составляющей вектора состояний 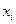 на начальное условие в момент
на начальное условие в момент 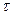 по
по 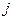 – ой составляющей
– ой составляющей  , равное 1. При этом начальные значения по остальным переменным состояния в момент
, равное 1. При этом начальные значения по остальным переменным состояния в момент 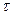 равны нулю, а входные воздействия на рассматриваемом интервале [
равны нулю, а входные воздействия на рассматриваемом интервале [ 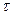 ,
, 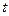 ] отсутствуют. Так для системы 2-го порядка:
] отсутствуют. Так для системы 2-го порядка:
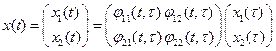 при
при 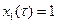 ,
,  ,
,
 ,
, 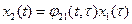 , т.е.
, т.е. 
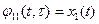 и
и 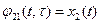
Физический смысл матрицы  следует из второго слагаемого: это реакция по
следует из второго слагаемого: это реакция по  –
–  -ой составляющей выхода в момент
-ой составляющей выхода в момент 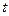 на воздействие по
на воздействие по 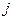 – ой составляющей вектора входа
– ой составляющей вектора входа  в виде единичной
в виде единичной  – функции в момент
– функции в момент 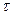 при нулевых начальных условиях и отсутствии воздействий по остальным составляющим входного вектора.
при нулевых начальных условиях и отсутствии воздействий по остальным составляющим входного вектора.
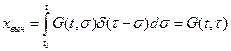 ,
, 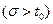 ,
, 

 .
.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 853; Нарушение авторских прав?; Мы поможем в написании вашей работы!